[edit 30.7. korjasin kadonneet kuvat]

Edellisessä artikkelissa keskityin Iteraatiolista-komennon käyttöön Verhulstin logistisen mallin bifurkaatiokaavion tuottamisen apuna. Tutkitaan Iteraatio ja Iteraatiolista -komentoja hieman tarkemmin.

Käytän tätä kirjoittaessani sekä GeoGebran 5 ja 6 versioita.

yksinkertainen syntaksi

Iteraatio-komennon kielioppi on yksinkertainen: Iteraatio( <Funktio>, <Alkuarvo>, <Iteraatioiden määrä> ). Iteraatiolista toimii samalla tavalla, mutta se palauttaa listan iteroinnin vaiheista. Listan ensimmäinen jäsen on alkuarvo. Niinpä listassa on n + 1 jäsentä, jos n on iteraatioiden lukumäärä. Yleensä näitä komentoja kannattaa käyttää vain Syöttökentän komentoina, varsinkin jos n on iso luku. Komentojen käyttö selvinnee alla olevasta CAS-esimerkistä.

Jos komennot kirjoittaa CAS:iin, niin silloin alkuarvona voi käyttää x:ää.

f(x) = {x, x^(2) – x, x^(4) – (2 * x^(3)) + x, x^(8) – (4 * x^(7)) + (4 * x^(6)) + (2 * x^(5)) – (5 * x^(4)) + (2 * x^(3)) + x^(2) – x, x^(16) – (8 * x^(15)) + (24 * x^(14)) – (28 * x^(13)) – (10 * x^(12)) + (60 * x^(11)) – (50 * x^(10)) – (14 * x^(9)) + (48 * x^(8)) – (20 * x^(7)) – (14 * x^(6)) + (12 * x^(5)) + (2 * x^(4)) – (4 * x^(3)) + x, x^(32) – (16 * x^(31)) + (112 * x^(30)) – (440 * x^(29)) + (1004 * x^(28)) – (1064 * x^(27)) – (756 * x^(26)) + (4212 * x^(25)) – (5340 * x^(24)) + (120 * x^(23)) + (7980 * x^(22)) – (9120 * x^(21)) + (120 * x^(20)) + (8880 * x^(19)) – (7236 * x^(18)) – (1566 * x^(17)) + (5871 * x^(16)) – (2352 * x^(15)) – (2040 * x^(14)) + (2064 * x^(13)) + (150 * x^(12)) – (960 * x^(11)) + (270 * x^(10)) + (270 * x^(9)) – (180 * x^(8)) – (24 * x^(7)) + (54 * x^(6)) – (8 * x^(5)) – (10 * x^(4)) + (4 * x^(3)) + x^(2) – x}

Iteraatiolistan avulla saa aikaiseksi kummallisia kuvioita.

Newtonin menetelmä

Tehdään pieni esimerkki Newtonin menetelmästä. Luodaan ensin liu’ut alkuarvolle ja kierrosten lukumäärälle n. Määritellään tutkittava funktio ja Newtonin menetelmän iteroitava lauseke.

Lasketaan n ensimmäistä iteraatiota. Luodaan sopivasti pisteitä ja murtoviiva, jotta saadaan parempi kuva iteraatiosta. Luodaan piste, joka näyttää iteraation viimeisen vaiheen.

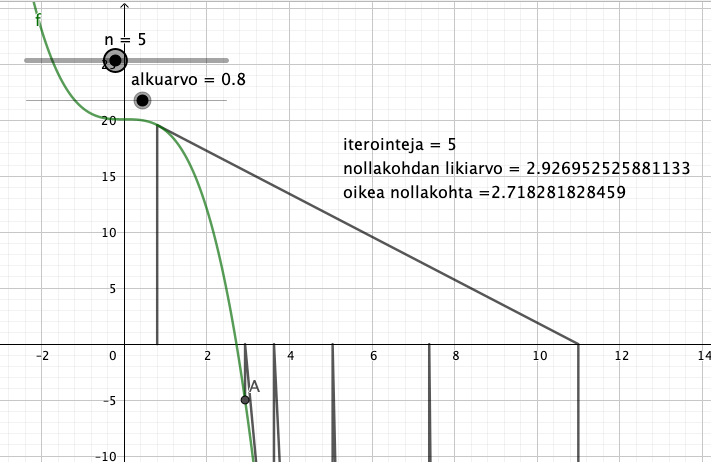
hieman monimutkaisempi kielioppi

Iteraatio-komento toimii myös siten, että muuttujana voi olla jokin GeoGebran olio, ei pelkästään matemaattinen funktio: Iteraatio( <Lauseke>, <Muuttujat>, <Alkuarvot>, <Lukumäärä> ). Alla oleva laskee viidennen Fibonacciluvun. 

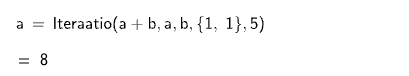
Kun tätä syntaksia käyttää, niin pitää muistaa, että iteroinnin tulee palauttaa sellainen objekti, joka sopii ensimmäiselle muuttujalle syötteeksi. Fibonacci-esimerkissä ensimmäinen muuttuja on luku (tai itse asiassa kaksi lukua).

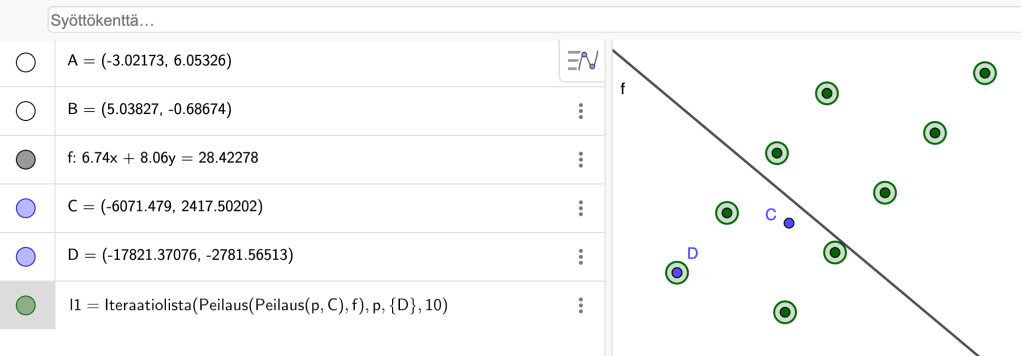
Seuraavassa esimerkissä Piirtoalueella on suora f ja pisteet C ja D. Komento

Iteraatiolista(Peilaus(Peilaus(p, f), C), p, {D}, 10)

peilaa pisteen D ensin suoran f  suhteen ja sitten suhteen pisteen C . Näin syntyy piste, jolle toistetaan nuo peilaukset.

Syntyvien vihreiden pisteiden perusteella vaikuttaa siltä, että kyseiset pisteet ovat kahdella yhdensuuntaisella suoralla. Todista.

Mitäköhän tapahtuu, jos peilauksen järjestystä vaihdetaan? Kokeile itse.

Lähteet

Iteraatio-komento GeoGebra manuaalissa
https://wiki.geogebra.org/en/Iteration_Command

Iteraatiolista-komento GeoGebra manuaalissa
https://wiki.geogebra.org/en/IterationList_Command

Newtonin menetelmä appi GeoGebra Materiaaleissa
https://www.geogebra.org/m/cqbaa4eh