-
Kolmioneliöiden pinta-alalauseet
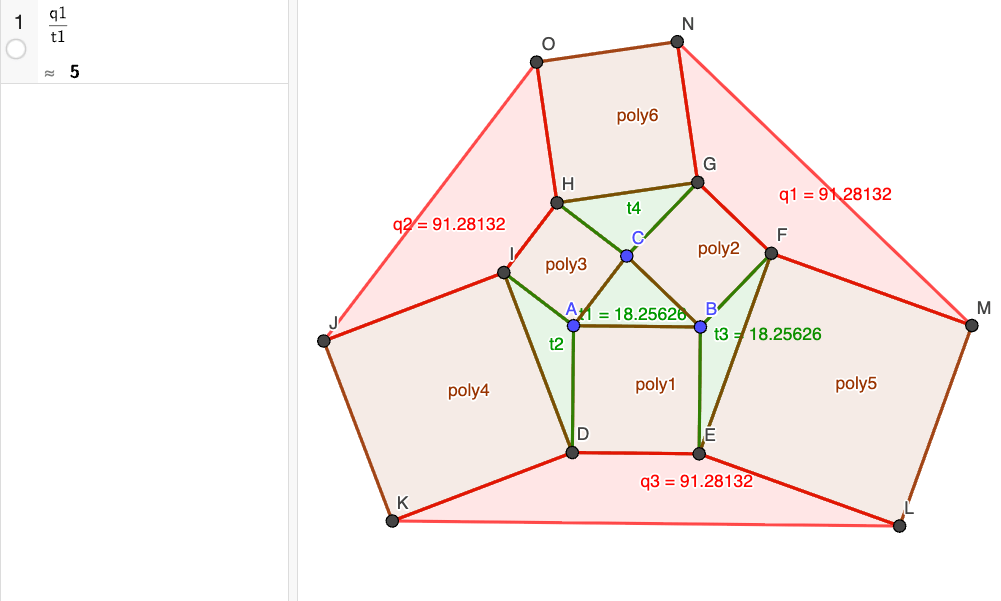
Jokin aikaa sitten kirjoitin artikkelin ”Melkein Pythagoraan lause”. Pythagoraan lauseen kuva jäi vaivaamaan mieltäni ja päätinpä tuottaa kolmion sivujen neliöt mielivaltaiselle kolmiolle ja jatkaa kuviota GeoGebran avulla. Seuraavassa joitain totuuksia, joita löysin. Ongelma. Todista Lauseet 1 – 7. Luodaan kolmio ABC, sen pinta-ala on t1. Luodaan kolmion sivuille nelikulmiot ABED,… Continue reading
-
Europass course in Helsinki
Last week I taught the course ”GeoGebra and Python for STEM and STEAM Teachers” at the new Europass Helsinki facilities on the Töölönlahti campus. I hope my students learnt some new things about GeoGebra and math scripting with Python. At least I learnt many things. My new Slovakian teacher friends. It… Continue reading

