MIKKO RAHIKKA

The electrical things have their lives too, paltry as those lives are.

Kumma integraali

Tämä löytyi Twitteristä John Goldenin retwiittaamana. Alunperin tämän julkaisi @EylemGercek. Pakkohan tätä oli kokeilla GeoGebrassa. Numeerinen integrointi tuotti saman tuloksen.

Alla kuva Eylemin tweetistä.

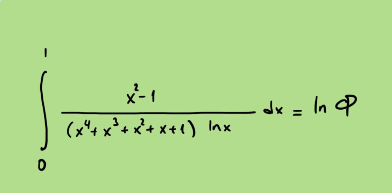
GeoGebran numeerinen integrointi vahvistaa tuloksen.

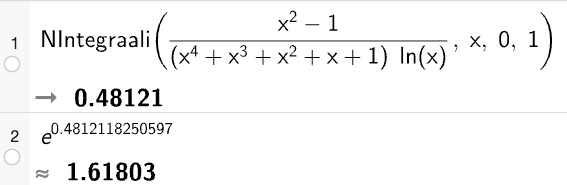
Leikin GeoGebralla ja kokeilin erilaisia integroimisvälejä. Lopulta muutin integroimisvälin oikean reunan äärettömäksi. 

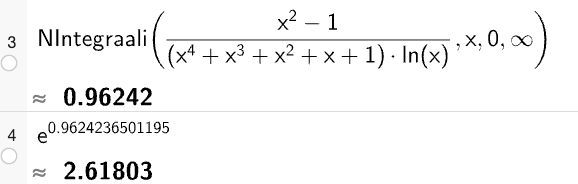
Joku integraalilaskentaa harrastava osannee laskea tarkat arvot ihan käsipelillä.

Eylemin integraali

\int_0^1\frac{x^2-1}{\left(x^4+x^3+x^2+x+1\right)\ln\left(x\right)}dx=\ln\left(\frac{1+\sqrt{5}}{2}\right)

Mikon integraali

\int_0^{\infty}\frac{x^2-1}{\left(x^4+x^3+x^2+x+1\right)\ln\left(x\right)}dx=\ln\left(\left(\frac{1+\sqrt{5}}{2}\right)^2\right)

Jätä kommentti

This site uses Akismet to reduce spam. Learn how your comment data is processed.

Mainokset