MIKKO RAHIKKA

The electrical things have their lives too, paltry as those lives are.

Värähtelevän jousen liikkeen simulointi Pythonilla – Leapfrog integrointi

Dynamiikan ilmiöiden simuloinnissa pyritään yleensä tuottamaan F = ma -yhtälön ratkaisu aika-paikka koordinaatistossa. Esitän tässä Leapfrog-integrointina kutsutun menetelmän, jonka avulla useissa tapauksissa saadaan melko tarkkoja arvioita kappaleen paikasta ajan suhteen.

Koska kiihtyvyys on paikan toinen derivaatta, niin matemaattisesti ollaan ratkaisemassa differentiaaliyhtälöä, joka on muotoa x’’(t) = f(x), toki yhtälön oikealla puolella voi olla muitakin termejä, kun otetaan huomioon vaikkapa liikettä vastustavat voimat. Tässä x’’(t) on kiihtyvyys ja f(x) on voima jaettuna massalla paikan funktiona. Yksinkertaisissa ongelmissa, kuten vaikkapa pystysuora heittoliike ilman ilmanvastusta on oikea puoli vakio. Niinpä ratkaisun simuloinnissa voi käyttää tasaisesti muuttuvan liikkeen kaavoja

\begin{align} a=&\frac{F}{m}\\ v\left(t\right)=&\ v_0+a\cdot t\\ x\left(t\right)=&\ x_0+v_0t\ +\frac{1}{2}at^2 \end{align}

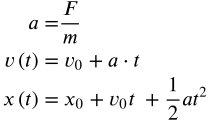
Simuloinnin kannalta nuo kaavat muutetaan muotoon

\begin{align} a_{i+1}=&\frac{F\left(x_i\right)}{m}\\ v_{i+1}=&\ v_i+a_{i+1}\cdot dt\\ x_{i+1}=&\ x_i+v_{i+1}dt\ +\frac{1}{2}a_{i+1}dt^2 \end{align}

Tässä dt on simuloinnissa käytetty aikaväli.

Simuloidaan edellisellä menetelmällä värähtelevän jousen liikettä. Valitsin jousen, sillä harmoniselle värähtelijälle on olemassa tarkka sinimuotoinen ratkaisu, jonka avulla voi tutkia simulointimenetelmä toimivuutta.  Seuraavassa koodissa on käytetty hyväksi sitä tietoa, että liikeyhtälön ratkaisu

\begin{align} -kx&=ma\\ \mathrm{eli}&\\ x''\left(t\right)&=-\frac{k}{m}x \end{align}


on

\begin{align} x\left(t\right)&=A\cdot\sin\left(\sqrt{\frac{m}{k}}t+\frac{\pi}{2}\right) \end{align}

kun alkupaikka ja alkunopeus ovat nollia.

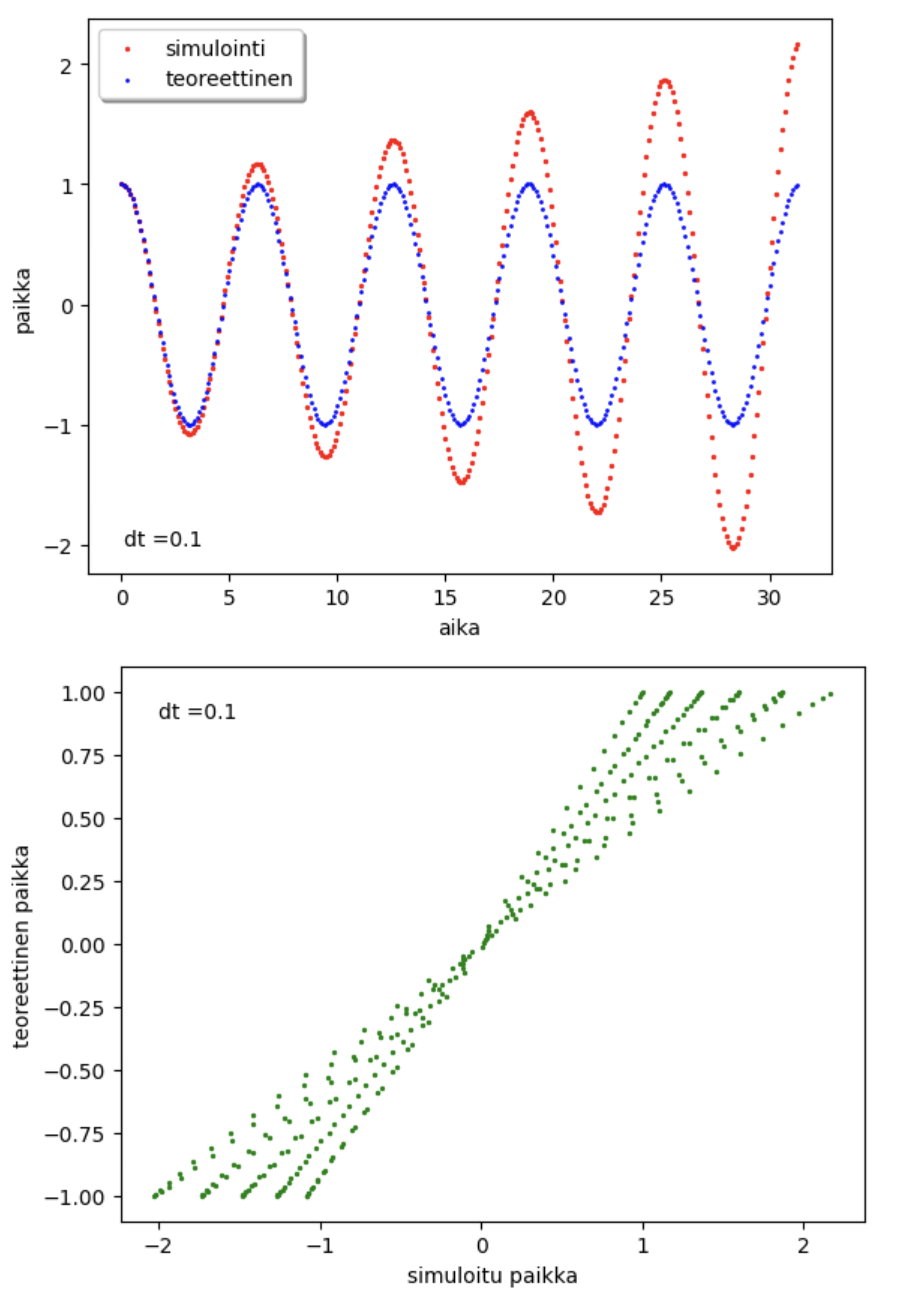
Näyttää siltä, että simulointi ”tuottaa lisää energiaa” liikkeeseen. Alempi kuvaaja kertoo lisää simuloinnin toimivuudesta. Mikäli simuloidut arvot ja teoreettiset arvot olisivat samoja, niin pisteet pysyisivät suoralla y = x. Mikäli riveillä 34 ja 35 vaihdetaan nopeuden ja paikan paikkoja, niin simulointi ”hävittää energiaa”.

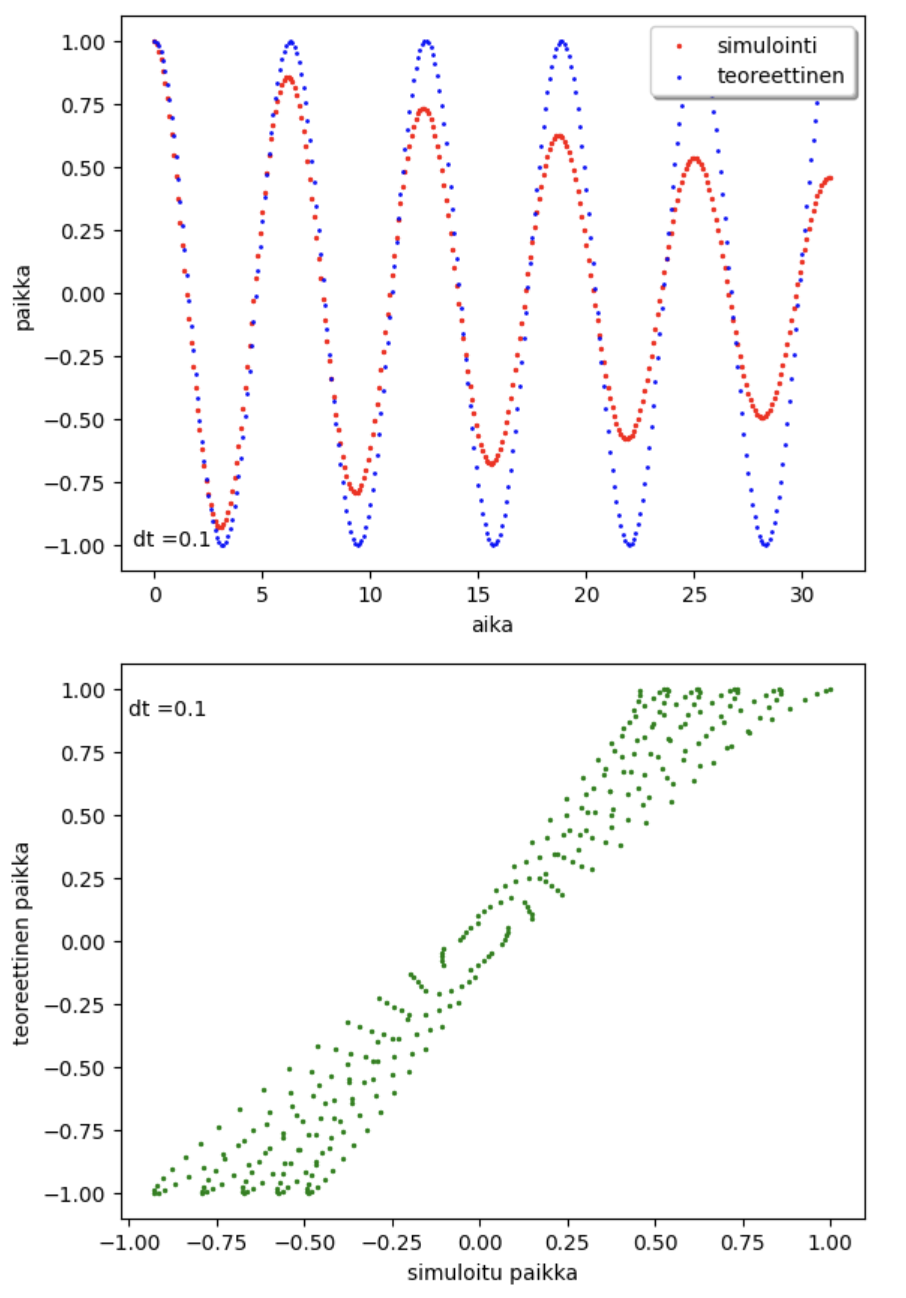
Muutetaan vielä alkuperäisen koodin aikaväli pienemmäksi, jotta nähdään sen vaikutus.

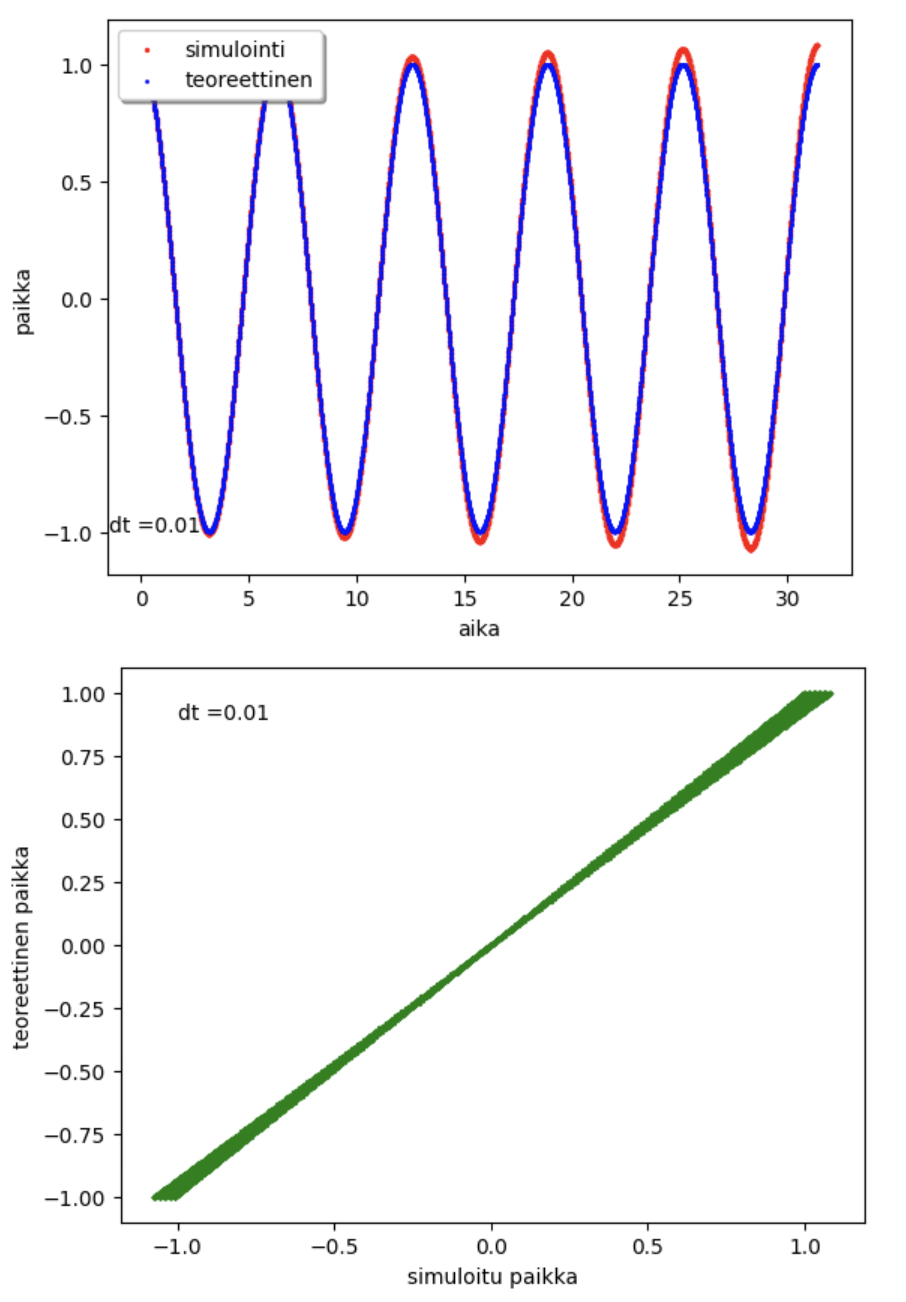
leapfrog integrointi

Edellisessä simuloinnissa virheen tuottaa se, että kiihtyvyys lasketaan aikavälin alussa. Kiihtyvyyden muuttuminen aikavälin aikana aiheuttaa virheen. 

Leapfrog-integrointi toimii siten, että lasketaan alkuarvojen avulla kiihtyvyys lopussa ja sen avulla nopeus käyttäen alku- ja loppukiihtyvyyksien keskiarvoa. Tässä hypätään kiihtyvyyden laskemisessa yhden aikavälin yli, siitä varmaankin on tullut tuo pukkihyppely-nimi. Kaavana integrointi näyttää tältä. 

\begin{align} a_i&=-\frac{k\ x_i}{m}\\ x_{i+1}&=x_i+v_i\cdot dt+\frac{1}{2}a_i\cdot dt^2\\ a_{i+1}&=-\frac{k\ x_{i+1}}{m}\\ v_{i+1}&=v+\frac{1}{2}\cdot\left(a_i+a_{i+1}\right)\cdot dt \end{align}

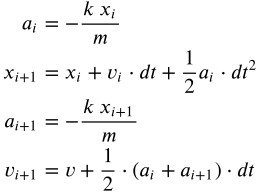
Koodissa ja kuvaajissa pukkihyppelyn käyttö näyttää tältä.

Pienemmällä aikavälillä dt = 0.01.

Lisätään jaksojen määrä kahteenkymmeneen. Nähdään, että simuloinnin ja teoreettisen mallin tuottamat arvot ovat lähes identtiset.

Pythonissa viimeisten paikkojen erotus on noin 7*10-6. Luku on laskettu Pythonin rivillä

Leapfrog-menetelmästä on monia eri versioita. Esitin tässä sen, jonka ymmärrän itse ja jonka osaan omasta mielestäni selittää. Se miten tätä menetelmää käyttää erilaisissa simuloinneissa riippuu tietysti käytetystä mallista. Lähteistä löytyy lisää luettavaa aiheesta.

Palannen aiheeseen lähiaikoina. Pitänee selvittää, miten tämän koodin saa toimimaan GeoGebran Pythonversiossa.

lähteet

Juttuun liittyvä Python-koodi Colabissa
https://colab.research.google.com/drive/1JIcqE5mECFpF3naFlH2CVHwfXQfs9blp?usp=sharing

Leapfrog integration Wikipediassa
https://en.wikipedia.org/wiki/Leapfrog_integration

The Leapfrog Numerical Method. Rhett Allain Wired lehdessä.
https://www.wired.com/2011/02/the-leapfrog-numerical-method/

Leapfrog integrator John Cookin blogissa
https://www.johndcook.com/blog/2020/07/13/leapfrog-integrator/Numeeriset menetelmät käytännössä.

Haataja ja muut. Hyvä suomenkielinen kirja.
http://users.jyu.fi/~merikosk/FNMmateriaalia/CSCnmk.pdf

Yksi vastaus artikkeliin “Värähtelevän jousen liikkeen simulointi Pythonilla – Leapfrog integrointi”

  1. Simulating harmonic motion with Leapfrog method and GeoGebra Python – Mikon fysiikka ja matikka avatar
    Simulating harmonic motion with Leapfrog method and GeoGebra Python – Mikon fysiikka ja matikka

    […] My original article in Finnishhttps://mikkorahikka.blog/2023/08/21/varahtelevan-jousen-liikkeen-simulointi-pythonilla-leapfrog-int… […]

    Tykkää

    Vastaus

Jätä kommentti

This site uses Akismet to reduce spam. Learn how your comment data is processed.

Mainokset