Jokin aika sitten tuotin a2 + b2 = c2 Pythagoraan kolmikoista (a, b)-pisteistön tasoon. Pisteistö näytti muodostavan ruudukon nelikulmioista, niinpä päätin tehdä pisteistön avulla ”shakkiruutu”-kuvioinnin. Samalla huomasin mielenkiintoisen ominaisuuden liittyen nelikulmioihin. Tarinaan liittyvä todistustehtävä sopinee lukiolaisille, joilla CAS-laskin on hallussa tai pitkäjännitteisyyttä kynän ja paperin kanssa.
Linkki edelliseen artikkeliin ja tarinassa esitetyt koodit löytyvät tämän artikkelin lopusta Lähteet-luvusta.
muistin virkistykseksi
Pythagoraan kolmikoilla tarkoitetaan lukukolmikoita (a, b, c), jotka on muodostettu seuraavalla tavalla. Olkoot m ja n ovat positiivisia kokonaislukuja, joille m > n. Tällöin luvut a = m2 – n2, b = 2mn ja c = m2 + n2 muodostavat Pythagoraan kolmikon. Pythagoraan kolmikot ovat sellaisia luonnollisia lukuja, joilla pätee Pythagoraan lause a2 + b2 = c2. Tällä tavalla luoduilla a, b, c kolmikoilla a < b < c.
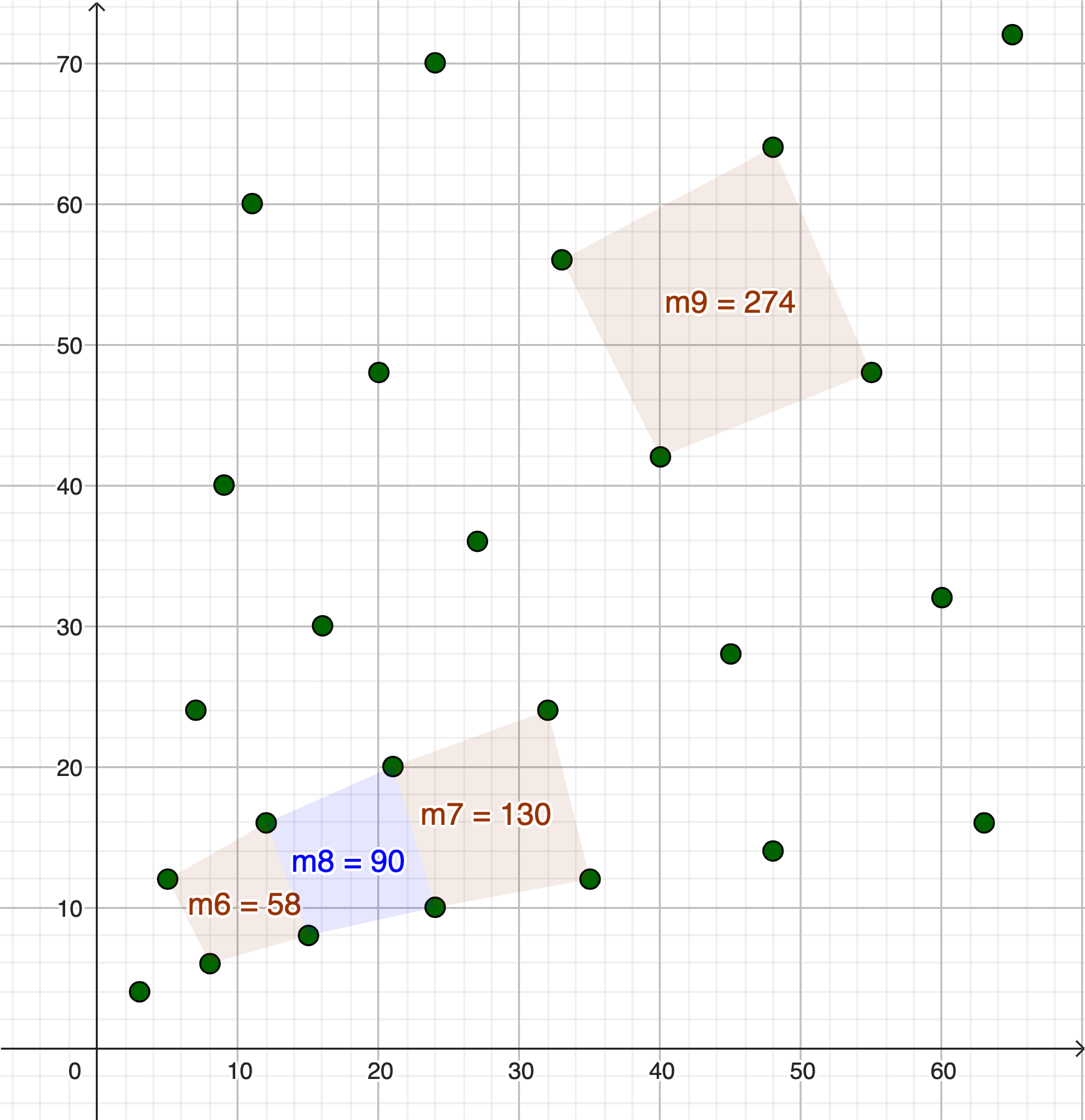
Alla kuva GeoGebran avulla tuotetusta pisteistöstä. Loin sinne myös joitakin nelikulmioita, tässä vaiheessa huomasin, että niiden pinta-alat näyttävät olevan luonnollisia lukuja. Miksi?
ongelma
Todista, että pisteistöön syntyvien monikulmioiden pinta-alat ovat luonnollisia lukuja. Nelikulmioiden syntymekanismi selitetään tarinan seuraavissa luvuissa.
shakkilautaruudutus GeoGebralla
Tuotin alunperin pisteistön GeoGebra 5:llä, niinpä päätin luoda nelikulmiot GeoGebra 6:lla. Ensin loin GeoGebran Algebra-ikkunaan funktiot f ja g, joiden arvolla tuotin a ja b- lukujen arvoja.
f(x,y)=x^(2)-y^(2)
g(x,y)=2 x y
Sen jälkeen käytin hieman kynää, paperia, aivojani ja yritystä ja erehdystä, jotta saisin pääteltyä shakkilautaruudutuksen nelikulmioiden kärkien koordinaatit.
Ensin loin muuttujan q ja tein siitä liu’un. Liu’un asetukset: Min = 1, Max = 100, Animaatiosakel = 1.
”Valkoiset” nelikulmiot sain yksinkertaisella komennolla
vnelikulmiot = Jono(Jono(Monikulmio((f(3+n+m,1+m),g(3+m+n,1+m)),(f(4+n+m,1+m),g(4+n+m,1+m)),(f(4+n+m,2+m),g(4+n+m,2+m)),(f(3+m+n,2+m),g(3+m+n,2+m))),n,0,q,2),m,0,q,1)
ja ”mustat”
mnelikulmiot = Jono(Jono(Monikulmio((f(3+n+m,1+m),g(3+m+n,1+m)),(f(4+n+m,1+m),g(4+n+m,1+m)),(f(4+n+m,2+m),g(4+n+m,2+m)),(f(3+m+n,2+m),g(3+m+n,2+m))),n,1,q,2),m,0,q,1)
Komennot tuttavat piirtoalueelle nelikulmioita ja samalla Algebra-ikkunaan niiden pinta-alat. Väritin nelikulmiot Piirtoalueen työkaluilla, kun muuttuja oli valittuna Algebraikkunassa.
Kun q = 5, niin

Vaikuttaa siltä, että pinta-alat ovat luonnollisia lukuja.

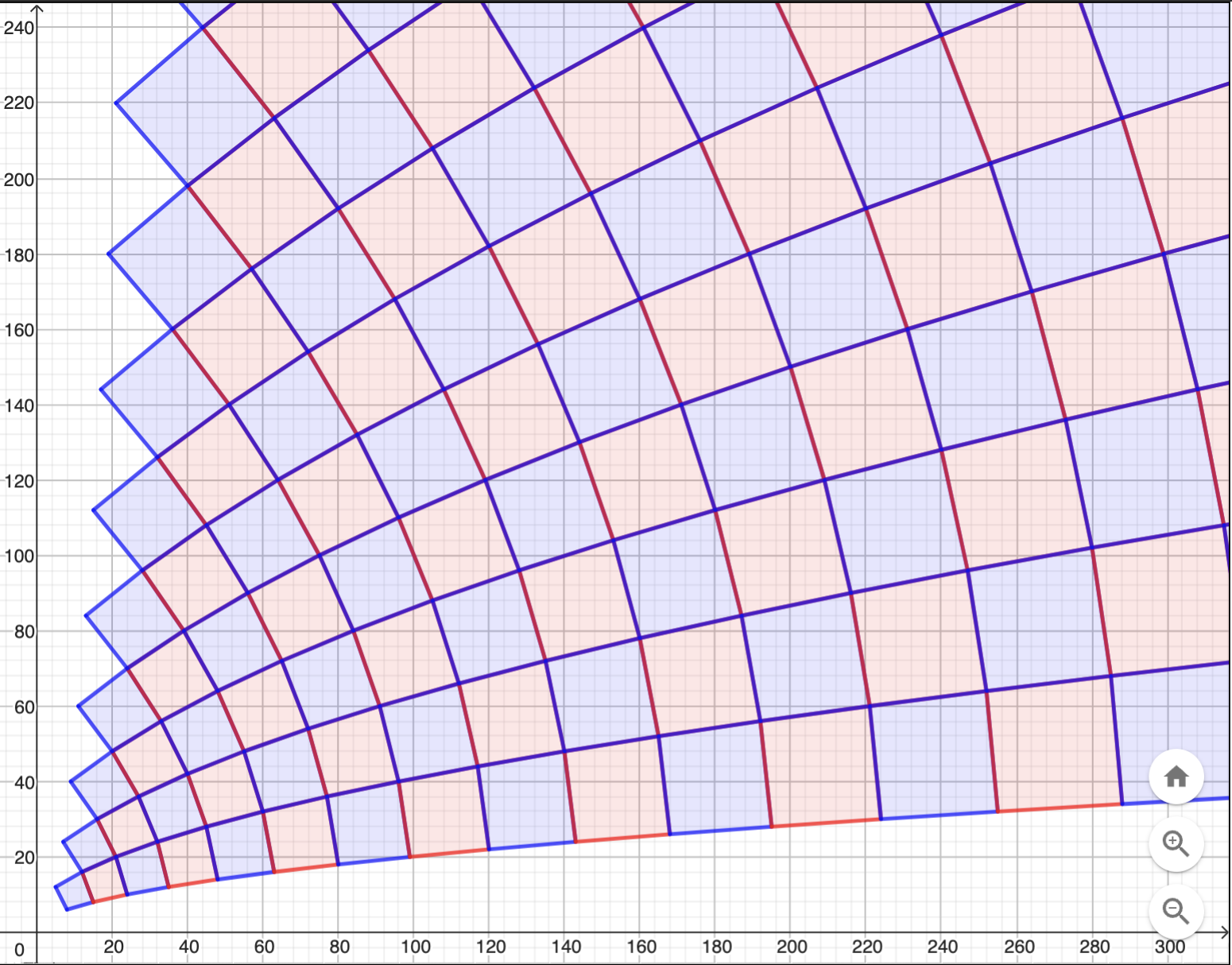
ruudutus GeoGebra Pythonilla
Päätinpä kokeilla myös uutta kehittelyvaiheessa oleva GeoGebra Python ohjelmointiympäristöä. Algoritmi on sama kuin GeoGebra-versiossakin. Tässä tosin muutin n-muuttujan muuttumaan yhden askeleen kerrallaan, vastaavasti pisteen koordinaateissa n on korvattu 2*n:llä.

Tämän tuottamisessa sain hieman apua Michael Borcherdsilta. Hän ehdotti, että lisään time-kirjaston sleep()-funktion (rivi 18), jotta ei tarvitse odottaa koko kuvan valmistumista, ennen kuin se tulee näkyville Piirtoalueelle.
Pisteet GeoGebran Piirtoalueelle Luodaan Point(x, y)-funktiolla, Pisteelle voidaan luoda erilaisia ominaisuuksia koordinaattien jälkeen (rivit 20 – 28). Tässä is_visible = False tarkoittaa, että piste ei näy Piirtoalueella. GeoGebran monikulmiot tuotetaan Polygon(kärkipistelista)- funktiolla, kärkipistelistan tulee olla Pythonin lista GeoGebrapisteistä (rivit 33 – 34).
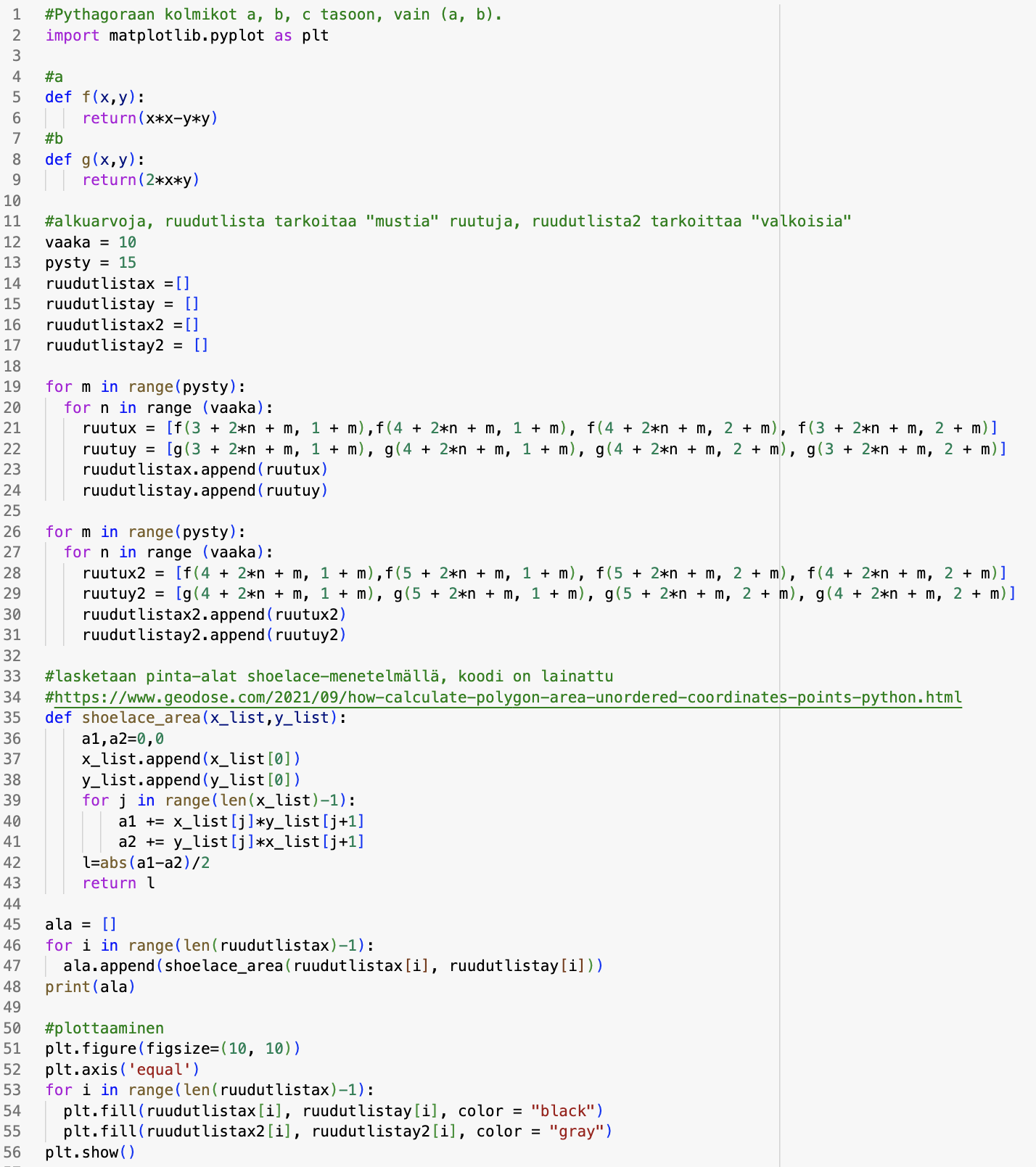
ruudutus perinteisellä Pythonilla ja matplotlibillä
Alla kuva samaan aiheeseen liittyvä koodi Pythonilla ja matplotlib-kirjastolla. Koska matplotlibin fill(x, y) vaatii muuttujikseen erikseen listat x-koordinaateista ja y-koordinaateista, koodi on hieman hankalammin luettavaa (rivit 54-55).
Laskin monikulmion pinta-alat Shoelace-kaavalla.
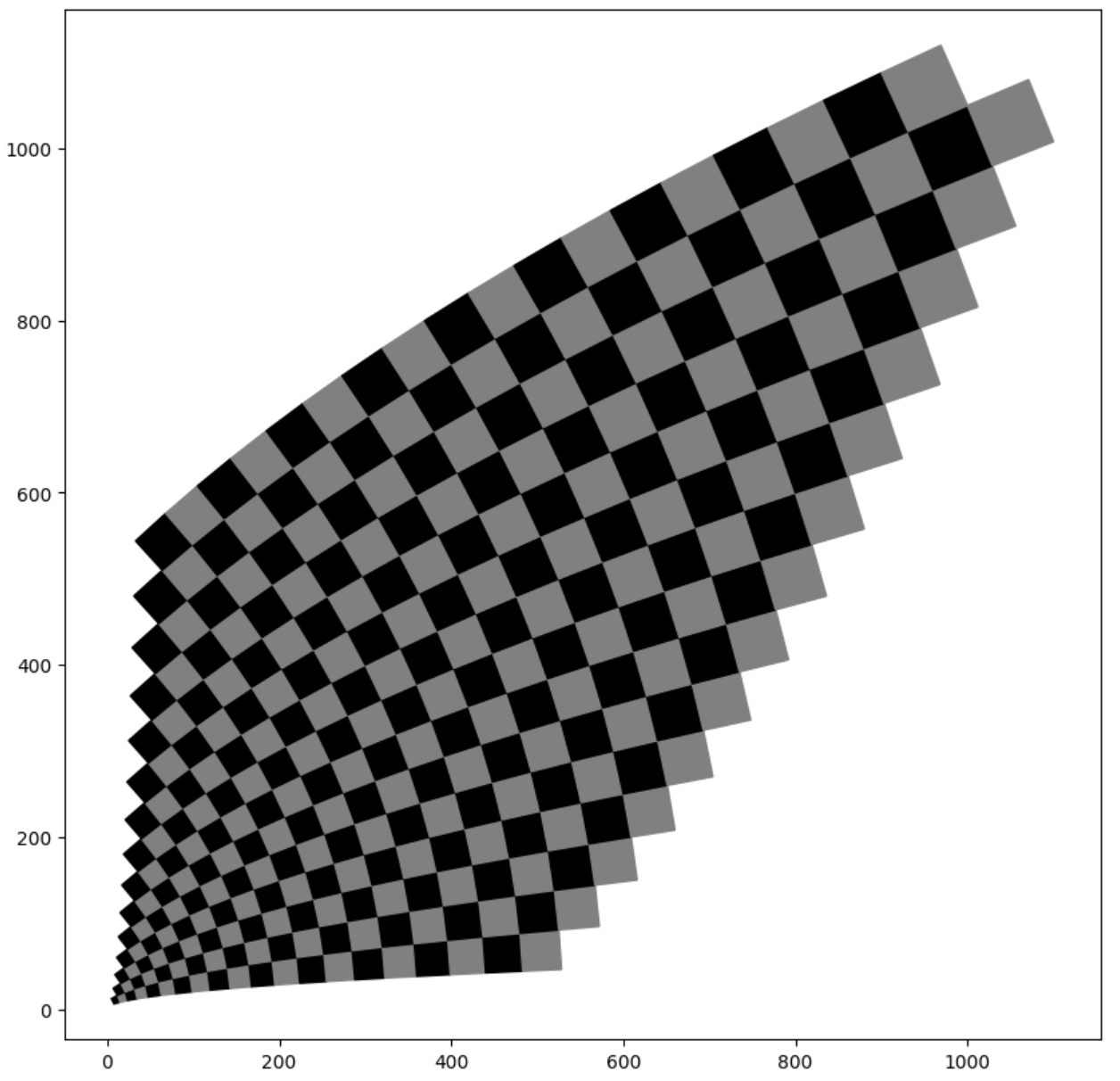
Alla Shoelace-koodin tuottamia pinta-aloja. Näyttää siltä, että ne ovat luonnollisia lukuja, miksi?
[58.0, 130.0, 234.0, 370.0, 538.0, 738.0, 970.0, 1234.0, 1530.0, 1858.0, 106.0, 194.0, 314.0, 466.0, 650.0, 866.0, 1114.0, 1394.0, 1706.0, 2050.0, 170.0, 274.0, 410.0, 578.0, 778.0, 1010.0, 1274.0, 1570.0, 1898.0, 2258.0, 250.0, 370.0, 522.0, 706.0, 922.0, 1170.0, 1450.0, 1762.0, 2106.0, 2482.0, 346.0, 482.0, 650.0, 850.0, 1082.0, 1346.0, 1642.0, 1970.0, 2330.0, 2722.0, 458.0, 610.0, 794.0, 1010.0, 1258.0, 1538.0, 1850.0, 2194.0, 2570.0, 2978.0, 586.0, 754.0, 954.0, 1186.0, 1450.0, 1746.0, 2074.0, 2434.0, 2826.0, 3250.0, 730.0, 914.0, 1130.0, 1378.0, 1658.0, 1970.0, 2314.0, 2690.0, 3098.0, 3538.0, 890.0, 1090.0, 1322.0, 1586.0, 1882.0, 2210.0, 2570.0, 2962.0, 3386.0, 3842.0, 1066.0, 1282.0, 1530.0, 1810.0, 2122.0, 2466.0, 2842.0, 3250.0, 3690.0, 4162.0, 1258.0, 1490.0, 1754.0, 2050.0, 2378.0, 2738.0, 3130.0, 3554.0, 4010.0, 4498.0, 1466.0, 1714.0, 1994.0, 2306.0, 2650.0, 3026.0, 3434.0, 3874.0, 4346.0, 4850.0, 1690.0, 1954.0, 2250.0, 2578.0, 2938.0, 3330.0, 3754.0, 4210.0, 4698.0, 5218.0, 1930.0, 2210.0, 2522.0, 2866.0, 3242.0, 3650.0, 4090.0, 4562.0, 5066.0, 5602.0, 2186.0, 2482.0, 2810.0, 3170.0, 3562.0, 3986.0, 4442.0, 4930.0, 5450.0]
lähteet
Aiheeseen liittyvä aiempi artikkelini ”Pythagoraan kolmikot tasossa GeoGebralla + ongelma”
https://mikkorahikka.blog/2023/10/21/pythagoraan-kolmikot-tasossa-geogebralla-ongelma/
Pythagorean chessboard GeoGebra-materiaaleissani https://www.geogebra.org/m/yxzx6dyp
GeoGebra Python koodi löytyy täältä
https://tinyurl.com/pyggb-pythag
Python + matplotlib koodi Colabissa https://colab.research.google.com/drive/1zIja2E2a6ifpRyb6jQPQZf-SAaLNQtSQ?usp=sharing
Shoelace equation Wikipediassa
https://en.wikipedia.org/wiki/Shoelace_formula

Jätä kommentti