Tosin ei tämä mikään uusi todistus ole, minä vaan en ole nähnyt sitä aiemmin. Tämä löytyi Futility Closetista. Oheinen todistus on käännetty Hollingdalen kirjasta.
Oletetaan, että neliöjuuri 2 on rationaaliluku. Tällöin
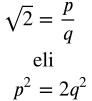
Jos yhtälön vasemman ja oikean puolen luvut jaetaan alkutekijöihin, niin luvuissa p2 ja q2 jokainen tekijä esiintyy kaksi kertaa. Näin ollen vasemman puolen luvulla p2 on parillinen määrä tekijöitä ja oikean puolen luvulla 2q2 on pariton määrä tekijöitä. Näin päädyimme ristiriitaan. Niinpä neliöjuuri 2 ei ole rationaaliluku.
MOT.
Kuten Futility Closetin artikkelin loppukaneetissa kerrotaan niin Hollingdalen mukaan tämä todistus on peräisin Antiikin Kreikasta, tosin hän ei kerro asiasta sen tarkemmin.
Wikipedian “Square root of 2” -artikkelissa on monta erilaista ratkaisua ja löytyipä sieltä tämäkin kohdasta ”Proof by unique factorization”.
Aika moni kirja kertoo, että ensimmäisen todistuksen yhteismitattomuudelle eli irrationaalilukujen olemassaololle esitti Hippasos Metapontialainen (eli noin 530 – 450 eaa.) . Kirjallisten lähteitteni mukaan Hippasoksen todistus oli koulukirjoistakin tuttu versio, jossa todistetaan että luvut p ja q ovat sekä parillisia, että parittomia.
Jossain vaiheessa pitää palata tähän aiheeseen, varsinkin kun yksi kuuluisa yhteismitattomuustodistus liittyy pentagrammikuvioon.
lähteet
Short Work Futilty Closetissa
https://www.futilitycloset.com/2023/12/20/short-work-4/
Martin Gardner. ”The Square Root of two = 1.41421 35623 73095….” Math Horizons. April 1997.
https://maa.org/sites/default/files/pdf/upload_library/22/Evans/april_1997_5.pdf
Stuart Hollingdale. Makers of Mathematics. Dover. 1989. Luku 2 Early Creek Mathematics, 6 The discovery of incommensurability.
Hippassos Wikipediassa.
https://en.wikipedia.org/wiki/Hippasus
Square root of 2 Wikipediassa
https://en.wikipedia.org/wiki/Square_root_of_2
Cut the Knot -sivuston Square root of 2 is irrational -sivu
http://www.cut-the-knot.org/proofs/sq_root.shtml
Carl Boyer. Tieteiden kuningatar, Matematiikan historia osa 1. Art House 1994. Luku 5 Sankarikausi, Yhteismitattomuus, Kultainen leikkaus.

Jätä kommentti