[edit. 18.3.24. korjasin kolmikkojen määrittelyn järkevämmäksi.]
Kun jossain näen ongelman, joka jotenkin liittyy Pythagoraan lauseeseen, niin päässäni alkaa pörrätä mehiläisiä. James Tantonin X-tweetissä oli simppeli kysymys. Onko ”käänteisellä” Pythagoraan lauseella 1/a2 + 1/b2 = 1/c2 ratkaisuja? Onhan sillä.
Tantonin alkuperäinen tweetti.
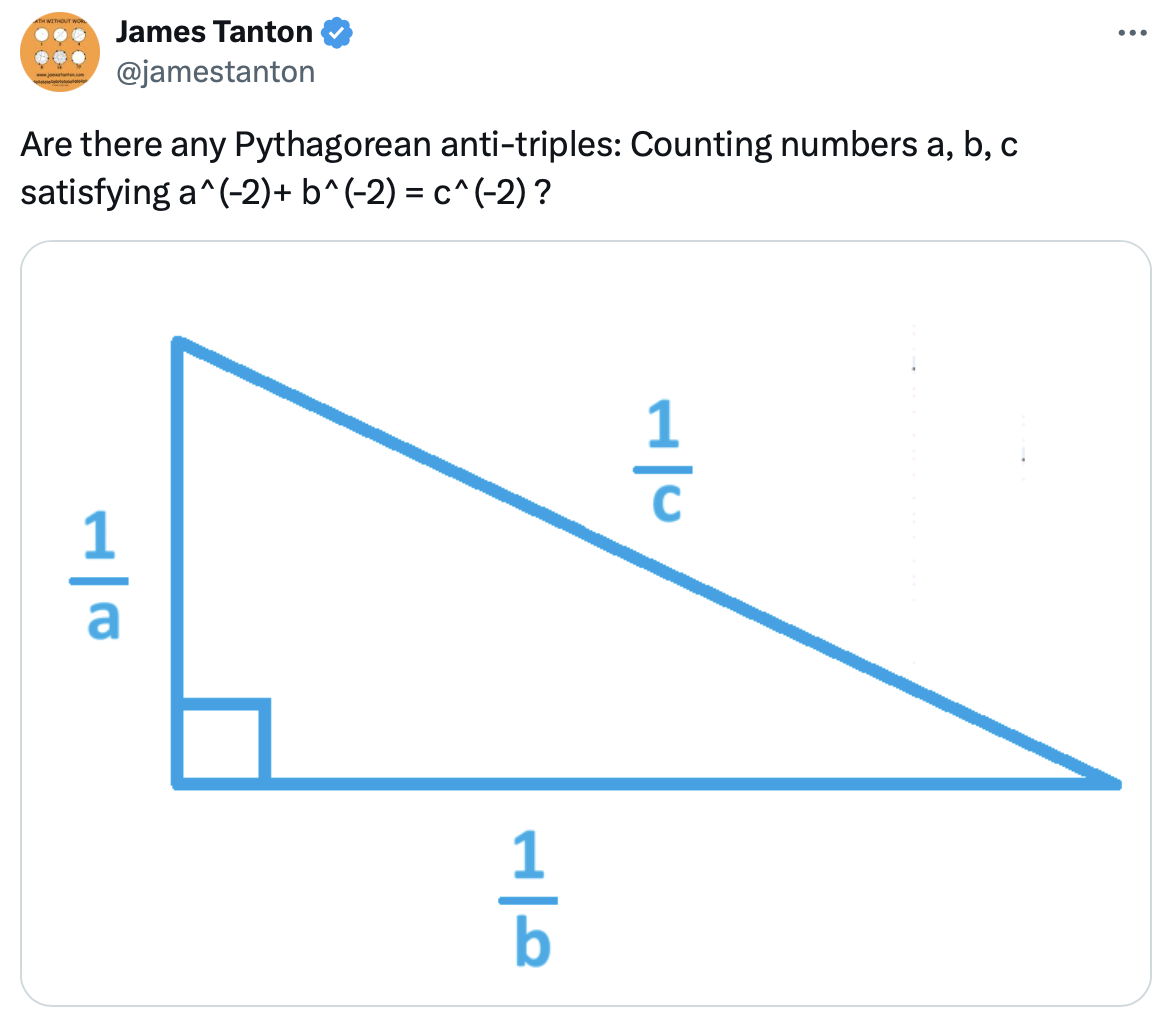
käänteiset Pythagoraan kolmikot
Käänteiset Pythagoraan kolmikot a, b, c ovat luonnollisia lukuja (1, 2, 3,…), joilla

Filosofit saavat pohtia, kelpaako (0, 0, 0) ratkaisuksi. Koska nollalla ei saa jakaa, niin minä hylkään ne..
ongelmia
Tweetissä oli aiheeseen liittyviä kommentteja, joista erityisesti Gonçalo Freitasin väite jäi mieleeni.

Suomeksi ongelma on seuraava. Tutkitaan Pythagoraan lauseen x2 + y2 = z2 ratkaisuja missä luvut x, y, x ovat kokonaislukuja > 0.
Gonçalon väite. Yhtälöllä x2 + y2 = z2 (x, y, z > 0) on kokonaislukuratkaisu (a, b, c) jos ja vain jos (bc, ac, ab) on yhtälön 1/(bc)^2 + 1/ (ac)^2 = 1/ (ab)^2 ratkaisu.

Ongelma 1. Onko Gonçalon väite totta? Jos on, niin todista. Jos ei, niin todista tai keksi vastaesimerkki.
Ongelma 2. Jos Gonçalon väite pitää paikkaansa, niin onko kolmikkojen (bc, ac, ab) lisäksi muita ratkaisuja yhtälölle 1/x^2 + 1/ y^2 = 1/ z^2
yleisempi ongelma
Tottakai tätä ongelmaa pitää tutkia. Tein ensin pienen testin GeoGebralla. Kun kirjoitin alla olevan komennon n:n arvolla 20, niin sain kaksi ratkaisua.
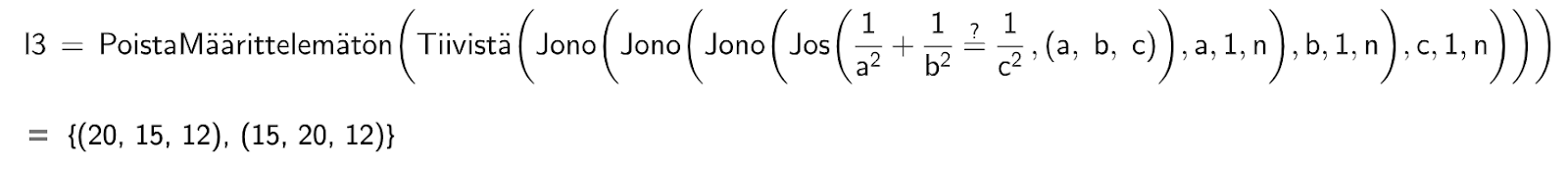
Löytyykö noita ratkaisuja lisää. Kirjoitin pienen Python koodinpätkän, jolla voi tutkia tällaisia ongelmia raa’an voiman menetelmällä. Tosin muokkasin koodin sellaiseksi, että ei tarvitse käyttää jakolaskua. Tutkin samalla ratkaisuja eri potenssien arvoilla yhtälössä.

Alla ratkaisuja kun suurin n:n arvo on 300.
Aika jännä pisteistö syntyy kun n = 1. Mitäköhän nuo kuvaajaan syntyvät suorat ovat?

Kun potenssi on 2, niin käänteisongelmassa ratkaisuja on aika harvassa verrattuna originaaliin Pythagoraan lauseeseen. Nuo suorat kiinnostavat?




Juolahtipa mieleen, että tässä on jotain tuttua.
Mikon suurehko lause
Yhtälöllä

ei ole kokonaislukuratkaisuja, kun x, y ja z > 2.
Todistus. Olen keksinyt väittämälle ihmeellisen todistuksen, mutta marginaalissa ei riitä sille tilaa.
Julkaisen todistuksen, kun löydän riittävän kokoisen marginaalin.
lähteet
James Tantonin X-tweetti
https://twitter.com/jamestanton/status/1767838258489155921
Fermat’n suuri lause
https://fi.wikipedia.org/wiki/Fermat%E2%80%99n_suuri_lause

Jätä kommentti