[edit. 4.1.25. korjasin vuosiluvun viimeisessä virkkeessä.]

Luku 2025 on mielenkiintoinen, kuten kaikki luvut. Päätinpä tutkia yhtälöiden x² + y² = 2025² ja  x² + y² + x²= 2025² kokonaislukuratkaisuja. Apuna käytin Pythonia ja GeoGebraa. Tein muutaman Python koodinpätkän, joiden avulla  tuotin taulukot, ratkaisut ja kuvaajat. Jos haluat itse katsella interaktiivisia kuvaajia, niin lähetä minulle sähköpostia m at mikkorahikka.blog ja pyydä Colab Python koodeja. Valitettavasti en osaa sijoittaa noita interaktiivisia kuvaajia tänne WordPressiin.

Yhtälön x² + y² = n² aidosti positiivisia kokonaislukuratkaisuja (x, y, n) kutsutaan usein Pythagoraan kolmikoiksi (Pythagorean Triplet) ja yhtälön x² + y² + x²= n² ratkaisuja x, y, z, n > 0 Pythagoraan nelikoiksi (Pythagorean Quadruple). 

2025-säteinen ympyrä

Pythagoraan kolmikot voi tulkita suorakulmaisiksi kolmioiksi, joissa kateettien pituudet ovat x ja y ja n on hypotenuusa. Jos ratkaisuksi hyväksytään kaikki kokonaisluvut, niin ratkaisut asettuvat n-säteisen ympyrän kaarelle. Toki kolmikot voisi tulkita myös suorakaiteiksi, joiden sivujen pituudet ovat x ja y, n on tällöin suorakaiteen lävistäjä.

Yhtälön x² + y² = 2025² aidosti positiiviset ratkaisut.

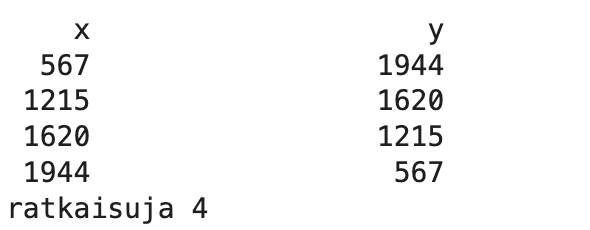
Kaikki ratkaisut xy-koordinaatistossa, näitä on 20.

Ongelma 1. Mikä on pinta-alaltaan suurin suorakulmainen kolmio, jonka kateetit ja hypotenuusa ovat Pythagoraan kolmioita (x, y, 2025)?

2025-säteinen pallo

Pythagoraan nelikot (x, y, z, n) voi tulkita suorakulmaisina särmiöinä, joiden sivujen pituudet ovat x, y, ja z, n on lävistäjän pituus.

Kun ratkaisin Pythagoralaiset nelikot n:n arvolla 2025 sain eri 3012 ratkaisua. Tässä yhteydessä annoin Googlen Colabissa Gemini tekoälyn auttaa kuvaajien piirrossa. Enää ei tarvitse Googletella miten Matplotlibin ja Plotlyn asetuksia muutetaan, kysyy vain Geminiltä ja se tuottaa tarvittavan koodin.

Kuvassa yhtälön  x² + y² + x²= 2025² ratkaisut, kun x, y, z ja n > 0. On hyvä huomata, että tässä määritelmässä x, y ja z ovat suurempia kuin nolla. Niinpä ratkaisuksi ei kelpaa Pythagoraan kolmikoiden x = 567, y = 1944, z = 0.

Alla kaikki kokonaislukuratkaisut. Lähimpänä olevat pisteet ovat tumman vihreitä ja taaempana vaaleampia.

Ongelma 2. Kuinka monta kokonaislukuratkaisua on yhtälöllä  x² + y² + x² = 2025²?

Tässä kuvassa on puolipallo, x >0..

Kun zoomaa lähemmäksi, niin pisteistössä näkyvät hahmot tulevat selvemmin esille. Miksiköhän niitä muodostuu?

Ongelma 3. Kuinka suuri on suurimman sellaisen  suorakaiteen tilavuus, jonka sivujen pituudet (x, y, z)  ovat yhtälön x² + y² + x²= 2025² kokonaislukuratkaisuja. Samalla kiinnostaa myös suurin tilavuus, jos hyväksytään myös irrationaaliratkaisut.

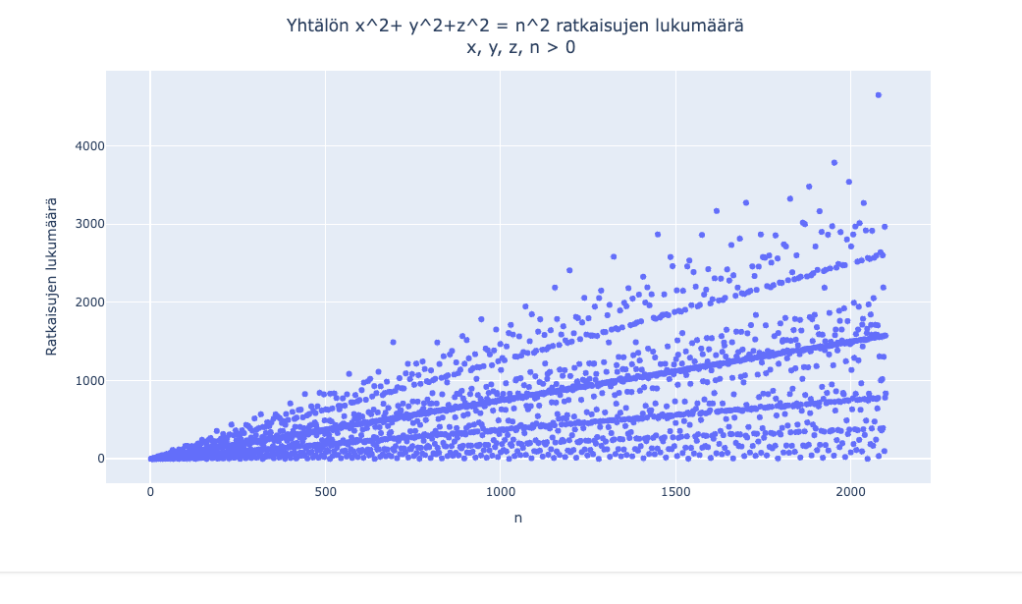
nelikkojen lukumäärä

Laskin Pythagoraan nelikkojen lukumäärän eri n:n arvoilla. Alla kuvaaja. Mitäköhän nuo suoran näköiset hahmot ovat?

Tässä hieman pidemmälle n:n arvoon 2100 saakka. Tuo kummallinen piste on n:n arvolla 2079. Pitänee tutkia sitä tarkemmin.

Hauskaa Uutta Vuotta :o)

lähteet

Pythagoraan kolmikko Wikipediassa
https://fi.wikipedia.org/wiki/Pythagoraan_kolmikko

Pythagorean quadruple Wikipediassa
https://en.wikipedia.org/wiki/Pythagorean_quadruple

Pythagorean triple Wikipediassa
https://en.wikipedia.org/wiki/Pythagorean_triple