Viisikanta ja siihen liittyvät totuudet ovat aina olleet lähellä sydäntäni. Törmäsin tähän Miquelin teoreemaan Futility Closetissa jokin aikaa sitten. Verkosta löytyi mielenkiintoisia artikkeleita aiheeseen liittyen. Pakkohan näitä oli tutkia. Samalla opiskelin GeoGebran käyttöä tällaisien kuvioiden piirtämisen apuna.

Monessa teoreemassa käytetään käsitettä konsyklinen. Pisteet ovat konsyklisiä, mikäli ne ovat saman ympyrän kehällä. Perusgeometria kertoo myös, että kolme pistettä (jotka eivät ole samalla suoralla) määrittävät ympyrän. Pentagrammilla eli viisikannalla tarkoitetaan tässä tarinassa sellaista geometriasta kuviota, joka syntyy viidestä tason pisteestä, jotka muodostavat tähtikuvion. Lukija voi pohtia mitä tarkemmin vaaditaan viideltä pisteeltä, että ne ylipäänsä voivat muodostaa tähtikuvion.

Yritän yksinkertaistaa lauseita niin että ne on helpompi ymmärtää. Täsmällisemmät matemaattiset määrittelyt löytyvät liitteistä. Niissä käytetään runsaasti alaindeksejä, jotka eivät avaudu kovin helposti. Käytän tässä värejä helpottamaan teoreemojen ymmärtämistä.

Miguelin pentagrammilause

Olkoon ABCDE (kuvassa siniset pisteet) viisikanta eli pentagrammi ja pisteet F, G, H, I, ja J (kuvassa vihreät pisteet) viisikannan sivujen leikkauspisteet. Muodostetaan viisi ympyrää (mustat ympyrät) siten, että ne kulkevat viisikannan kärkipisteen ja kahden lähimmän leikkauspisteen kautta. Esimerkiksi ympyrä, joka kulkee pisteiden A, F ja J kautta. Ympyrät leikkaavat pareittain toisensa myös uloimmissa pisteissä K, L, M, N ja O (punaiset pisteet). Tällöin pisteet K, L, M, N ja O sijaitsevat saman ympyrän (punainen ympyrä) kehällä eli ne ovat konsykslisiä.

Ranskalainen Auguste Miquel (1816-1851 ) julkaisi kolmioon liittyvän teoreemansa 1838. Vuonna 2023 Norbert Hungerbühler ja kumppanit julkaisivat alkuperäiseen Miquelin lauseeseen liittyviä todistuksia. He käyttivät todistuksissa kompleksitasoa. Samalla löytyi uusia totuuksia aiheeseen liittyen.

Miquelin viiden ympyrän ja 10 konsyklisen pisteen pentagrammilause

Olkoon pisteet A, B, C, D ja E (punaiset pisteet) samalla ympyränkaarella eli konsyklisiä. Muodostetaan nämä pisteet keskipisteinä ympyröitä (mustat ympyrät) siten, että ne leikkaavat pareittain toisensa ja ulommat leikkauspisteet (mustat pisteet) ovat samalla ympyränkaarella kuin keskipisteet. Olkoot sisemmät leikkauspisteet F, G, J, H ja I (vihreät pisteet). Muodostetaan suorat vierekkäisten pisteiden kautta, suorien leikkauspisteet K, L, M, N ja O (siniset pisteet) ovat viiden mustan ympyrän kehillä.

Takadan lause

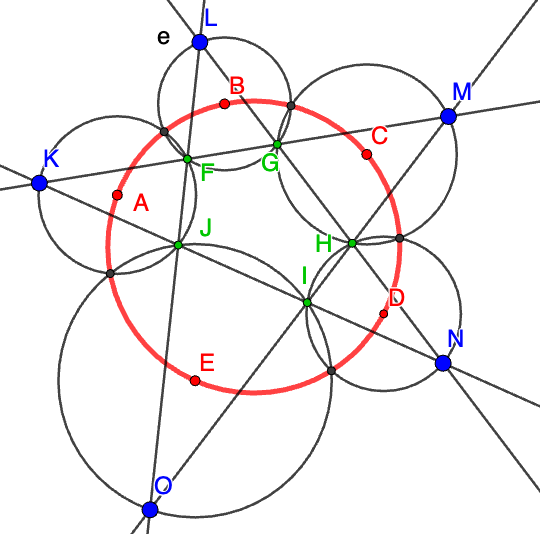
Olkoon ACEBD pentagrammi, jonka kärjet (siniset pisteet) ovat konsyklisiä eli saman ympyrän kehällä. Olkoot F, G, H, I ja J pentarammin sivujen leikkauspisteet (vihreät leikkauspisteet). Muodostetaan viisi ympyrää (punaiset ympyrät) siten, että niiden kärjet kulkevat kahden vierekkäisen pentagrammin kärjen ja niiden ”välissä” olevan sivujen leikkauspisteen kautta. Ympyrät leikkaavat pareittain pentagrammin kärjissä ja sisemmissä pisteissä K, L, M, N ja P (mustat pisteet).  Tällöin sisemmät pisteet ovat myös konsyklisiä (musta ympyrä).

Japanilainen lukiolainen Hideyuki Takada löysi tämän totuuden vuonna 1989. Samana vuonna Tominosuke Otsuki ja Kazuo Masuda todistivat teoreeman kahdellakin eri tapaa. Trigonometriaan perustuva todistus on noin 10 sivua ja analyyttiseen geometriaan perustuva todistus noin 6 sivua pitkä. Jätän todistusten tarkemman tutkimisen lukijan harteille.

Tran Quang Hungin yhdentoista ympyrän lause

Tämä lause on aika haastava, niinpä esitän sen pala kerrallaan.

Valitaan viisi pistettä (siniset pisteet) siten, että ne muodostavat konveksin viisikulmion.

Jatketaan viisikulmion sivuja suoriksi (punaiset suorat). Suorien leikkauspisteet (punaiset pisteet) ja niiden väliset janat muodostavat pentagrammin.

Muodostetaan viisi ympyrää (vihreät ympyrät ja keskipisteet) siten, että ne kulkevat kahden vierekkäisen viisikulmion pisteen ja niitä vastaavan pentagrammin kärjen kautta. 

Nämä ympyrät leikkaavat toisensa myös ulommissa pisteissä (harmaat pisteet).

Muodostetaan viisi sellaista ympyrää (mustat ympyrät ja keskipisteet), että ne kulkevat kahden pentagrammin vierekkäisen kärjen (punaiset) ja niiden välissä olevan ulomman leikkauspisteen (harmaa) kautta.

Luodaan viisi suoraa (kuvassa mustat janat), jotka  kulkevat mustien ympyröiden keskipisteiden  ja vastakkaisella puolella olevien vihreän ympyröiden keskipisteillä. Suorat/janat leikkaavat samassa pisteessä (keltainen piste).

Tämän lauseen keksi vietnamilainen opiskelija Tran Quang Hung vuonna 2019. Artikkelissaan hän esittää myös lisää vastaavankaltaisia totuuksia.

Julkaisen omat tiedostoni GeoGebra-materiaaleissa kunhan olen siistinyt niitä tarpeeksi.

lähteet

Miquel’s Pentagram Theorem Futility Closetissa
https://www.futilitycloset.com/2025/07/29/miquels-pentagram-theorem/

Tominosuke Otsuki ja Kazuo Masuda, Certain Theorems on Pentagons, vuoden 1989 todistus Tanakan lauseelle
https://tus.repo.nii.ac.jp/records/1556

Tran Quang Hungin artikkeli vuodelta 2019 arXivissa: SOME NEW THEOREMS ON PENTAGON AND PENTAGRAM
https://arxiv.org/pdf/1908.00974

”Simppeli” todistus Miquelin teoreemalle kompleksilukujen avulla. Lorenz Halbeisen, Norbert Hungerbühler* and Vanessa Loureiro. The Pentagon Theorem in Miquelian Möbius Planes
https://dergipark.org.tr/en/pub/iejg/issue/80270/1255469

Lisää sotkuisia ympyröitä vuodelta 2023 Journal of Geometry -lehdessä. Norbert Hungerbühler. The lively siblings of the Pentagon theorem
https://link.springer.com/article/10.1007/s00022-023-00683-5

Auguste Miquel ranskankielisessä Wikipediassa
https://fr.wikipedia.org/wiki/Auguste_Miquel

GeoGebra Materiaaleissa on runsaasti työkirjoja Miquelin lauseeseen liittyen
https://www.geogebra.org/search/miquel

Konveksi joukko Wikipediassa
https://fi.wikipedia.org/wiki/Konveksi_joukko