Edellisessä tarinassani pohdin, millä todennäköisyydellä kahdella satunnaisesti valitulla luvulla ei ole yhteisiä tekijöitä. Tässä tutkiskelen kuvaajissa näkyviä hahmoja.
Kun katsoo edellisen artikkelin GeoGebra-kuvia, niin näkee, että joillain a:n arvoilla pisteitä on vähemmän ja joillain enemmän. Kun a on alkuluku, niin tällöin tietysti pisteitä on enemmän.
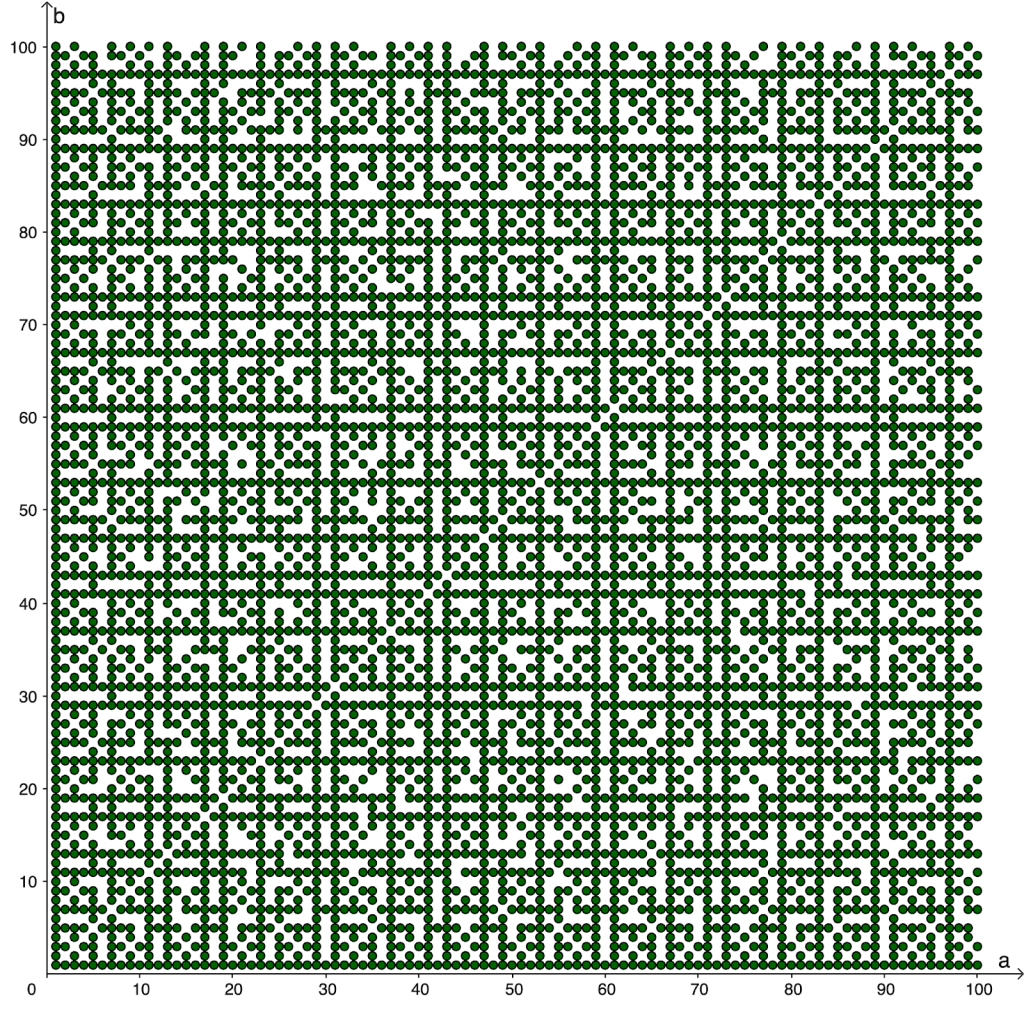
Seuraavassa kuvassa on pisteparit (a, b) merkitty, jos niillä ei ole yhteisiä tekijöitä, kun a ja b saavat kaikki arvot 1, 2, …, N. Tässä N = 100. Joillain a:n arvoilla (ja tietysti samoilla b:n arvoilla) pisteitä on paljon, joillain vähemmän. Pysty- ja vaakasuunnassa näkyy suoria, joissa on paljon pisteitä ja suoria, joissa pisteitä on vähemmän.
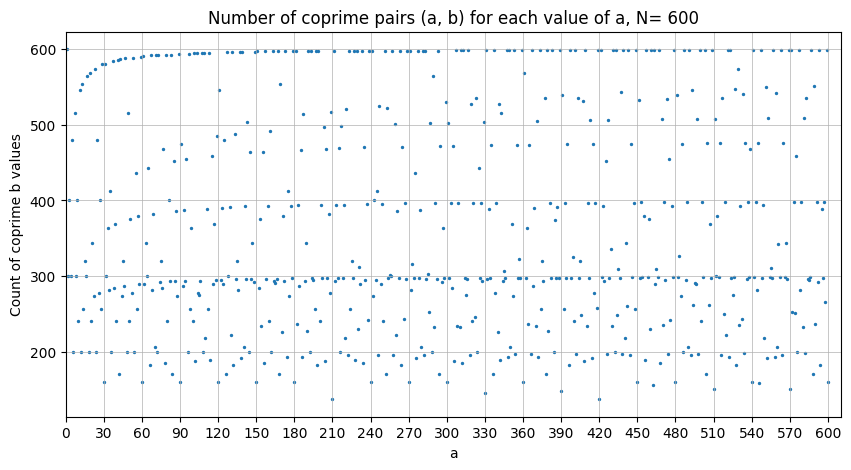
Laskin GeoGebralla kutakin a:n arvoa vastaavien pisteiden lukumäärän ja piirsin tuloksesta pylväsdiagrammin, kun N = 200.

Kuvaajasta näkee, että joka kuudes tolppa näyttäisi olevan matalammalla kuin muut. Lisäksi joka 30. näyttäisi olevan erityisen matala tolppa. Tietysti myös joka toinen eli parilliset luvut tuottavat matalampia tolppia verrattuna parittomiin.
Tässä vaiheessa siirryin tutkimaan ongelmaa Pythonin avulla. Koodaaminen on suht’koht’ nopeaa varsinkin, kun käyttää tekoälyä apuna. Vaihdoin myös kuvaajien otsikot englanninkielisiksi, en kelpuuttanut Gemini-AI:n suomenkielisiä versioita. Toisaalta tuo coprime on mukavan lyhyt verratuna ”keskenään jaottomiin lukuihin” tai ”lukuparit, joilla ei ole yhteisiä tekijöitä”.
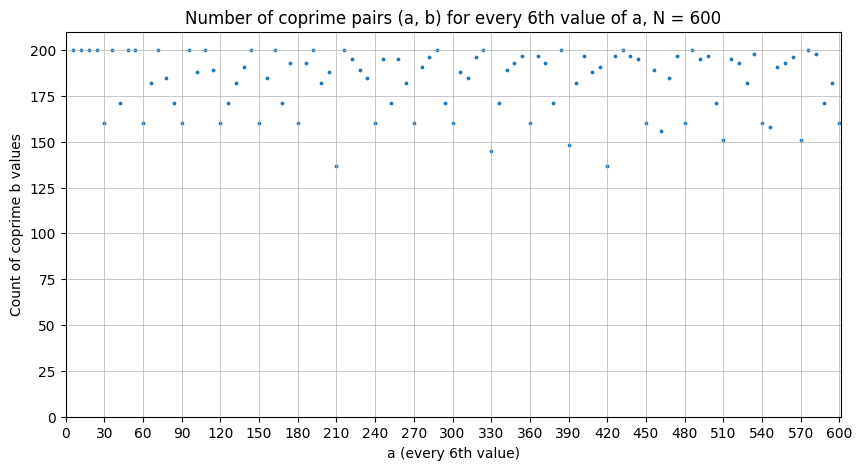
Seuraavasta kuvaajasta havaitaan, että joka kuudes arvo on suuruusluokkaa 200 tai jonkin verran alle ja joka kolmaskymmenes noin 160.
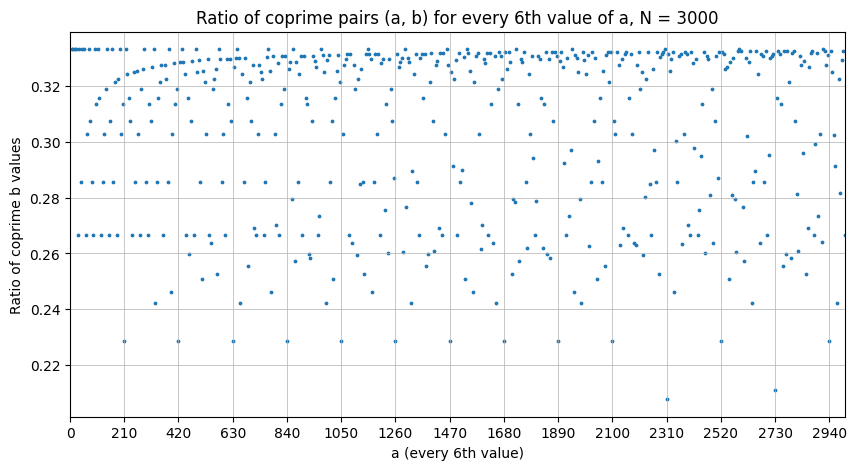
Seuraavassa kuvassa on mukana vai joka kuudes: 6, 12, 18, … Tässä havaitaan uusi kummallisuus 210!
Tutkitaan vielä suuremmilla N:n arvoilla.
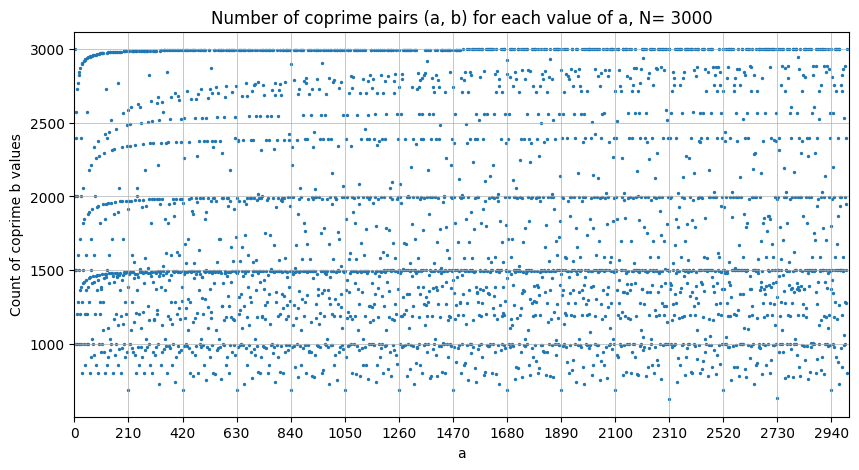
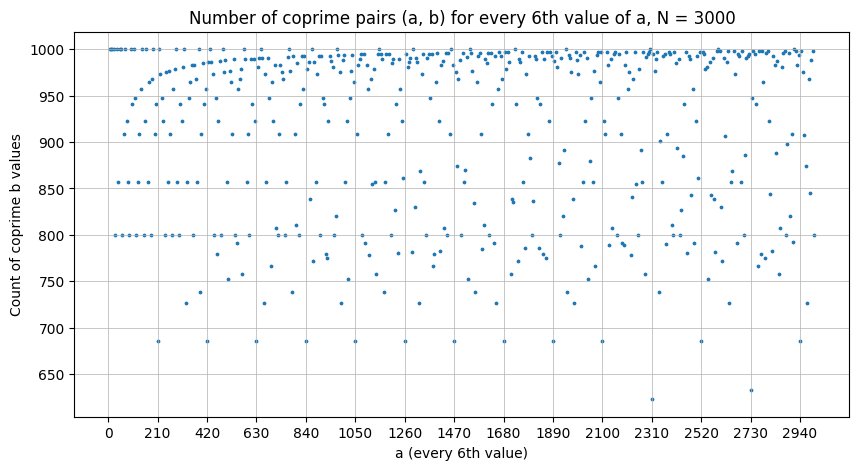
Hypoteesi 210:lla jaollisista luvuista pitänee paikkansa.
Tässä vaiheessa havaitaan, että 2310 tuottaaa pieniä arvoja suhteeseen. Kokeillaan.
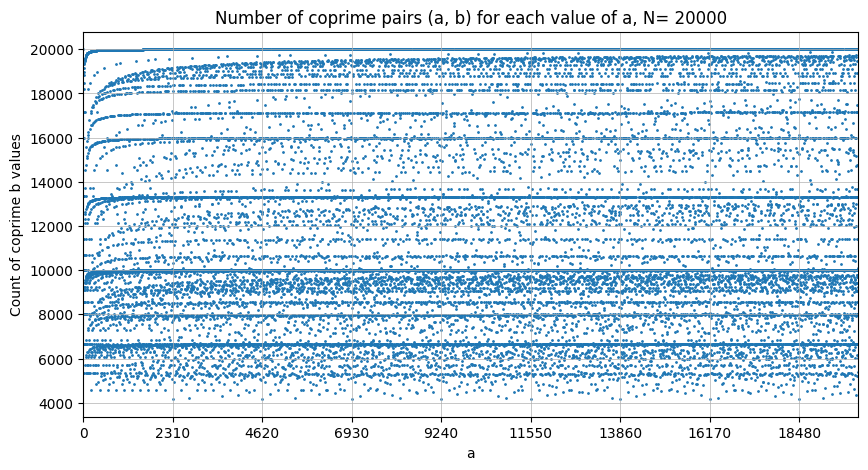
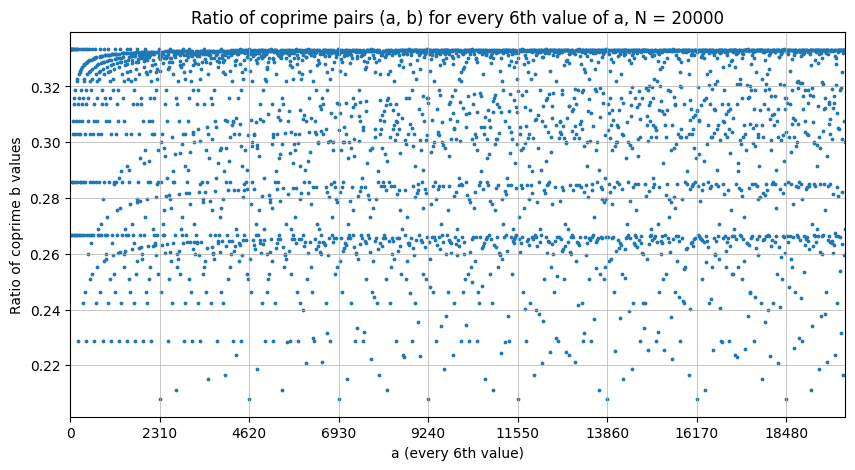
Tässä vaiheessa laskenta-aika alkaa olla isohko. Jätän kokeilemisen tässä vaiheessa tähän. Nyt pitäisi oikeasti alkaa pohtia ongelmia.
Ongelma 1. Miksi kuudella jaollisilla luvuilla on suhteellisen vähän sellaisia lukuja, joiden kanssa niillä ei ole yhteisiä tekijöitä?
Ongelma 2. Miksi luvuilla 30, 210 ja 2310 jaolliset luvut ovat sellaisia, että niillä on aika vähän sellaisia lukuja, joiden kanssa niillä ei ole yhteisiä tekijöitä?
Arvaan/tiedän, että seuraava tällainen luku on 30030.
pari pythonin sympy-funktiota
Tässä vaiheessa tarinaa pitää ottaa käyttöön pari alkulukuihin liittyvää funktiota: prime ja primorial. Molemmat funktiot löytyvät Pythonin SymPy-moduulista. On hyvä huomata, että ylioppilaskokeen Pythonissa ei ole SymPy-kirjastoa, tosin taitava koodari ohjelmoi funktiot helposti itsekin.
Funktio prime(n) tuottaa n:n alkuluvun.

Koulumatikasta tuttu funktio on kertoma. Kertoma(n) = factorial(n) = n! on lukujen 1, 2, 3, … n tulo. Niinpä 5! = 1*2*3*4*5=120. Primorial on vastaava funktio kuin kertoma, mutta tuloon otetaan vain alkulukuja.
Primorial(n) on n:n ensimmäisen alkuluvun tulo. Näin ollen primorial(5) = 2*3*5*7*11 = 2310.

Primorial-funktiota merkitään usein kertoman tapaan #-merkinnällä, 3# = 2*3*5 = 30.
jatketaan laskentaa
Nuo edellä ilmaantuneet luvut 2, 6, 30, 210 ovat ensimmäisten alkulukujen tuloja eli n#:n arvoja.
Valitsin N:n arvoksi 8# = 9699690. Laskin keskenään jaottomien lukuparien (a, b) lukumäärän ja jaoin sen N:n arvolla 9699690. Näin sain laskettua kyseisillä luvuilla keskenään jaottomien lukuparien (a, b) suhteellisen osuuden, kun a = n#.
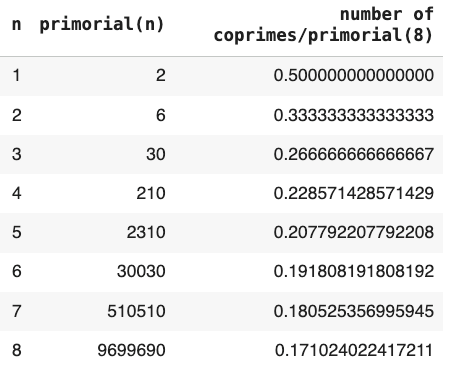
Alempaa kuvaajaa tuottaessani laskin suhdeluvun vain luvun n# arvoon saakka, edellisessä taulukossa kutakin n:ää kohden laskin arvoon 8#. Molemmissa tapauksissa tuli sama tulos.
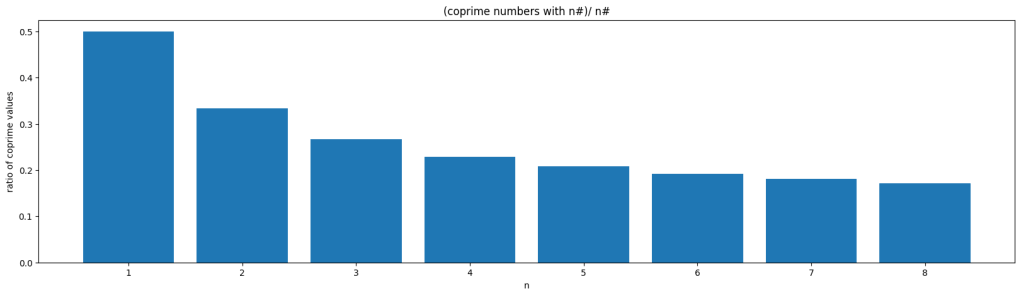
Mitä nuo suhteen arvot ovat? Kun taulukkoa ja (a, b) parien jaollisuutta pohtii hetken, niin mieleen saattaa juolahtaa, että suhde saadaan käyttämällä todennäköisyyslaskennasta tuttua komplementtien tuloa tyyliin.
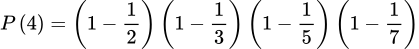
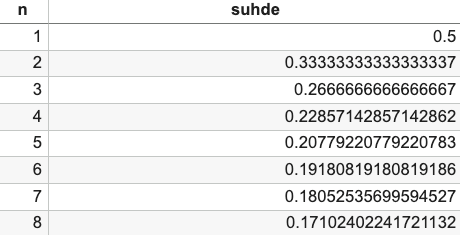
Lasketaan Pythonilla vastaavia arvoa. Sarakkeella suhde on laskettu komplementtien tulo edellä esitetyllä tavalla.
Ongelma 3. Todista. Tutkitaan lukupareja (a, b), missä a ja b saavat kaikki arvot 1, 2, …, N. Lasketaan niiden lukuparien (a, b) lukumäärä, joilla ei ole yhteisiä tekijöitä keskenään eli SYT(a, b) = 1 ja jaetaan tämä lukumäärä luvulla N#. Jos a saa arvot 1#, 2#, 3#, …, n#, niin kyseinen suhde on suuruudeltaan

Kaavassa luku M on n:s alkuluku. Toinen tapa esittää asia olisi kysyä: Millä todennäköisyydellä satunnaisesti valittu luku ei ole jaollinen luvulla n#, kun n saa arvot 1, 2, 3, …?
Mitäköhän tuolle P(n):n arvolle tapahtuu, kun n kasvaa isoksi? Lähestyykö tulo jotain nollaa suurempaa lukua kohden vai onko raja-arvo nolla?
Ongelma 4. Kuinka suuri on
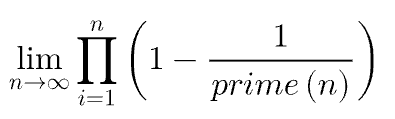
Nyt kun oivalsin suhteen arvon n#-luvuilla, niin tajusin, että sama ajattelu pätee muihinkin lukuihin. Jos minua kiinnostaa tietää kuinka suuri osuus luonnollisista luvuista ei ole jaollisia luvulla 540 = 2*2*3*3*3*5, niin lasken

Eli tulo lasketaan samalla tavalla kuin alkulukujen tuloillakin. Komplementtituloon otetaan tutkittavan luvun alkutekijöistä vain yksi.
Ongelma 5. Todista edellinen totuus. Tosin, jos olet todistanut ongelman 3, niin todistus on jo valmis.
Kun kirjoitin näitä tarinoita, niin mieleeni muistui viime vuonna lukemani kirjat du Satoyn The Music of Primes ja John Derbyshiren Alkulukujen lumoissa. Jos olet kiinnostunut tämän kaltaisien ongelmien historiasta, niin kehotan tutustumaan noihin kirjoihin.
Mikäli haluat tutustua tarinassa käytettyihin Python koodeihin, niin lähetä minulle sähköpostia.
lähteet
Primorial Wikipediassa
https://en.wikipedia.org/wiki/Primorial
Primorial Math Worldissa
https://mathworld.wolfram.com/Primorial.html
Sympy primorial
https://docs.sympy.org/latest/modules/ntheory.html#sympy.ntheory.generate.primorial
SymPy prime
https://docs.sympy.org/latest/modules/ntheory.html#sympy.ntheory.generate.prime
Andrew Booker The Nth Prime Page
https://t5k.org/nthprime/index.php#nth
Kirjat 2024 blogissani
https://mikkorahikka.blog/2025/01/01/kirjat-2024/

Jätä kommentti