Tällä viikolla ilmestyneessä xkcd:ssä käsitellään taivaankappaleen sädettä, jotta sammakko hypätessään ei putoaisi takaisin kappaleen pinnalle. Tutkitaan asiaa hieman tarkemmin.

Tässä Randall Munroe olettaa, että kun sammakko hyppää ylöspäin, sen nopeus on 4,5 m/s. Tämä nopeus on aika lähellä ihmisen maksiminopeutta kun ponnistetaan ylöspäin. Guinnessin ennätysten kirjan mukaan Darius Clark hyppäsi vuonna 2022 1,27 m:n korkeuteen. Tämä vastaa nopeutta 4,95 m/s, jolla Darius irtosi Maasta.
Kaavan johto on aika suoraviivainen, jos muistaa liike-energia ja gravitaation potentiaalienergian kaavan. Jotta sammakko putoaisi takaisin kappaleen pinnalle, niin

Tuossa m on sammakon massa, v pystysuora nopeus, jolla se irtoaa kappaleen pinnalta, G gravitaatiovakio ja M taivaankappaleen massa. Tietysti pitää olettaa, että kappale on pallosymmetrinen eikä pyöri.
Jos Maapallon säde kasvaisi noin 40 miljardin km:n pituiseksi massan pysyessä muuttumattomana, niin sammakko ja ihminen (avaruuspuvuissaan ja hengityslaitteissaan) voisivat yhdessä hypätä pois tältä pallolta.
Kun pohdiskelin tätä, niin muistuipa mieleeni ongelma liittyen pakonopeuteen eri säteisten ja tiheyksisien asteroidien pinnalta.
Laskeskelin GeoGebrassa tiheyden ja rajanopeuden välistä riippuvuutta, kun pystysuora lähtönopeus on 4,5 m/s.
Alla oleva kuvan perusteella näemme, että jos olemme kiviasteroidilla (tiheys noin 3000 kg/m3), jonka säde on alle 3,5 km, niin pääsemme pois asteroidilta hyppäämällä. Jos työskentelet jääplaneetalla, jonka säde on alle 7 km, niin ole varovainen kun hyppelet.
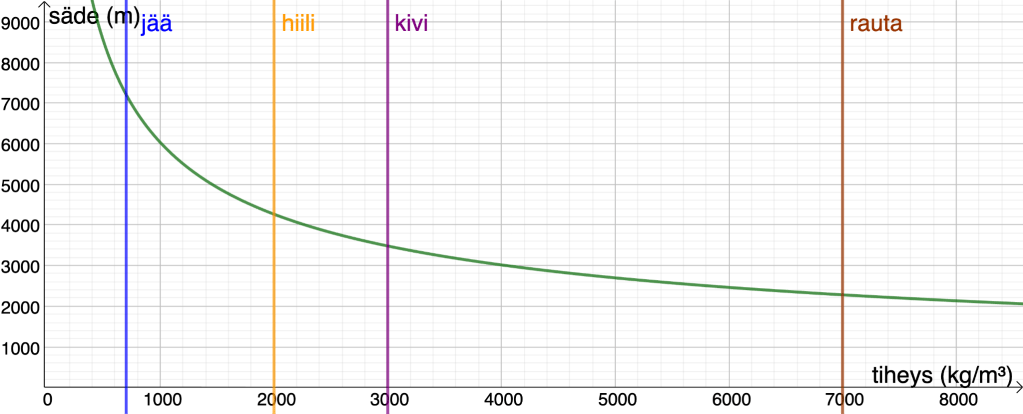
Ongelma. Olkoon asteroidi on homogeeninen, pallon muotoinen eikä se pyöri. Pohditaan, mikä on kappaleen säteen, tiheyden ja pakonopeuden välinen riippuvuus. Osoita, että rajasäde, jotta pallon pinnalta pääsee hyppäämään siten, ettei putoa takaisin pallon pinnalle, on suoraan verrannollinen nopeuteen ja kääntäen verrannollinen kappaleen tiheyden neliöjuureen.
Kun olin piirtänyt tuon kuvaajan GeoGebrassa, niin tajusi, että minähän osaan piirtää xkcd-tyyppisiä kuvaajia Pythonilla.
Alla matplotlibin plt.xkcd()-funktion avustuksella tehty kuvaaja.

lähteet
Jumping Frog Radius
https://xkcd.com/3181/
Highest vertical leap (running start) Guinnessin ennätysten kirjassa
https://www.guinnessworldrecords.com/world-records/95867-highest-vertical-leap-running-start
Kuvaajia Pythonin Matplotlib kirjastolla + xkcd-kuvaajat
https://mikkorahikka.blog/2024/03/02/kuvaajia-pythonin-matplotlib-kirjastolla-xkcd-kuvaajat/
Pakonopeus Wikipediassa
https://fi.wikipedia.org/wiki/Pakonopeus
Sama englanniksi, mutta hieman laveammin selitettynä
https://en.wikipedia.org/wiki/Escape_velocity

Jätä kommentti