[edit. 17.2.25 korjasin vialliset kuvaajatiedostot.]

Luin kirjan nimeltä ”Why do buses Come in Threes?”. Kirjassa on paljon tarinoita tosielämän matemaattisista ilmiöistä. Siinä oli selitetty muun muassa miksi biljardin/snookerin pitkissä lyönneissä vaikeinta on saada pallo pussitettua, kun kohdepallo on noin puolessa välissä  lyöntipalloa ja pussia. En ollut tyytyväinen kirjan esittämään kaavaan. Piti laskea itse.

Tässä tutkitaan vain suoraa lyöntiä, jossa lyöntipallo lyödään ilman kierteitä kohdepallon keskipistettä kohden. Jätän vaikeampien lyöntien analysoinnin lukijan harteille :o)

Kuvassa on kaksi samankokoista ja massaista biljardipalloa, lyöntipallo pisteessä A ja kohdepallo pisteessä B. Suora AB on kohtisuorassa vallia vastaan. Täydellisessä lyönnissä lyöntipalloa lyödään kohden palloa A siten, että se koskettaa kohdepalloa pisteessä T siten, että T on suoralla AB. Tällöin pallo osuu kohteeseen (valliin tai vaikka keskelle pussia) pisteessä H, joka on suoralla AB.

”Epätarkassa” lyönnissä lyöntipallon suuntakulma on α. Tällöin kohdepallon suuntakulmaksi tulee β. Kohdepallo osuu valliin pisteessä I. Merkitään poikkeamaa verrattuna tarkkaan lyöntiin eli janan HI pituutta kirjaimella m.

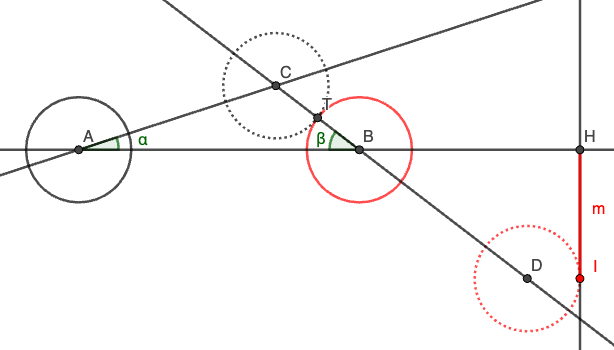
Ongelma. Olkoon b lyöntipallon ja kohdepallon keskipisteiden etäisyys (kuvassa janan AB pituus), p  lyöntipallon keskipisteen ja kohteen välinen etäisyys (AH), w pallojen säde  ja  α lyöntipallon suuntakulma. Luo malli joka kuvaa poikkeaman m suuruuden α:n, b:n, p:n ja w:n funktiona.

”Why do buses Come in Threes?”-kirjan kaava oli

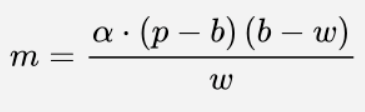
Kirjan kaava perustuu siihen, että kulma α on tosimaailmassa pieni. Alla oman mallini kuvaajat, b:n funktiona, kun p = 150 cm, w = 5,25 cm ja kulma α saa arvot 0,05°, 0,10°, 0,15° ja 0,20°. Punainen käyrä on piirretty kirjan kaavalla.

Kuten kuvaajasta näkyy oma mallini (vihreä) ja kirjan malli (punainen) ovat hyvin lähellä toisiaan. Alla vielä kuvaaja,  jossa lyöntikulma on 2°. Kovin paljon kulmaa ei voi kasvattaa, sillä sitten lyöntipallo ei enää osu kohdepalloon koko matkalla.

Piirsin kuvaajat GeoGebralla, käytin mallinnuksen apuna GeoGebra CAS:ia. Nyt kun tämä on ratkaistu, niin joskus pitää palata tähän aiheeseen ja tutkia tilannetta, jossa kohde ei ole samalla suoralla kuin lyöntipallo ja kohdepallo. Toisaalta kyytipallotkin muodostavat mielenkiintoisen ongelman.

lähde

Rob Eastway, Jeremy Wyndham. Why do buses Come in Threes? Portico. 2020.