Tämä löytyi ystäväni Timin X-tweetistä. Toki tämä ongelma on keksitty ja ratkaistu jo 1600-luvulla. Minulle tämä oli uusi juttu.
Ongelma 1. Olkoon ABC kolmio. Piirretään kullekin sivulle tasasivuiset kolmiot ABD, BCE ja CAF. Tällöin janat AE, BF ja CD leikkaavat samassa pisteessä. Todista.
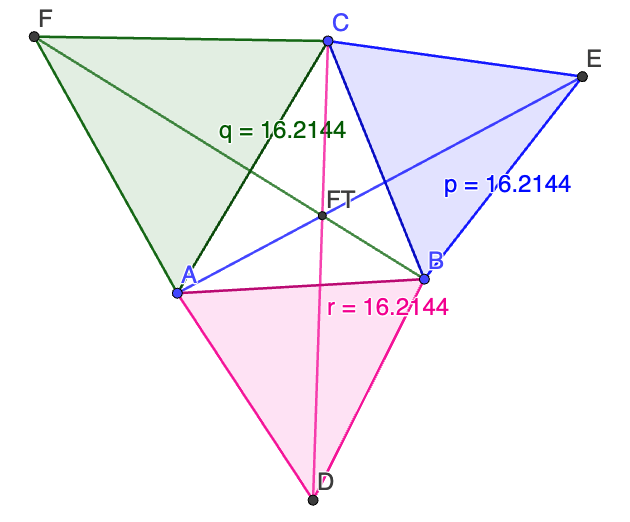
Lause toimii, vaikka piste olisi kolmion ulkopuolella, toki silloin lauseen janat pitää korvata suorilla.
Ongelma 2. Todista, että janojen pituudet AE, BF ja CD ovat yhtä suuret.
Ongelma 3. Todista, että janojen AE, BF ja CD välinen kulma on 120°.
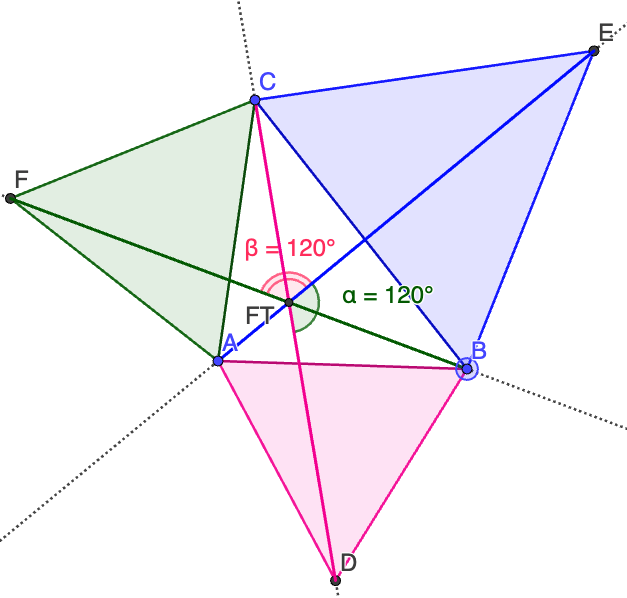
Ongelma 4. Olkoon kolmion sivujen pituudet a, b, ja c. Todista, että janojen AE, BF ja CD pituus on kolmion sivujen pituuksien geometrinen keskiarvo eli ![\left|AE=\right|BF=\left|CD\right|=\sqrt[3]{a·b·c}](https://lh7-rt.googleusercontent.com/docsz/AD_4nXdZidcM_s4S7JE8Y6pXmxftryAQP5TGIxVctjLzGa_ZdQW2Q9jU2ygLb2Q4yKChCE1NuR_nUZvY2yej3hthouX8IU3ft_AVkcjCz12wM11Rb7R6mOMjQ2CsLyehwU2OwalmOd8Zuw?key=UassOpcKK8UfU7oIjsnaIkXd){kind=small}
Ongelma 5. Olkoon FT on janojen AE, BF ja CD leikkauspiste. Tällöin FT on se piste, johon kärkien etäisyyksien summa on pienin.
Ongelma 6. Minkä nimisten henkilöiden mukaan piste FT on nimetty?
lähde
Tim Brzezinskin Youtube-video aiheesta
https://www.youtube.com/shorts/PvR9t_6dtHI
Jätä kommentti