Kuulin alun perin tämän tehtävän virolaiselta ystävältäni Hannes Jukkilta. Hänen ongelmansa liittyi Tallinnassa sijaitsevaan Väike-Öismäe Tiik nimiseen lampeen ja sitä kiertäviin ympyrän muotoisiin katuihin. Pohditaan millainen reitti on lyhin kahden saman kadun varrella olevan paikan välillä.

Tehtävä on julkaistu vuonna 1969 Levinien kirjassa Matemaatika ülesannete kogu keskkoolile.

Minusta tuo reitti ACBD pitää olla ACDB. Muokkaan ongelman omalle mielelleni sopivaksi. 

Ongelma 1. Muodostetaan kaksi samankeskistä ympyrää. Olkoon ympyröiden keskipiste on Ö ja säteiden pituudet 50 m ja 70 m. Pisteet A ja B ovat isommalla ympyrällä. Piste C on ÖA säteen ja pienemmän ympyrän leikkauspiste. Piste D säteen ÖB ja pienemmän ympyrän leikkauspiste. Pisteestä A voi kulkea kahta reittiä pisteeseen B, joko ulompaa reittiä eli  ympyrän kaarta AB pitkin (punainen) tai sisempää reittiä jana AC, ympyrän kaari CD, jana DB (sininen). Kuinka suuri kulman AÖB tulee olla, jotta reittien pituudet ovat yhtä suuret?

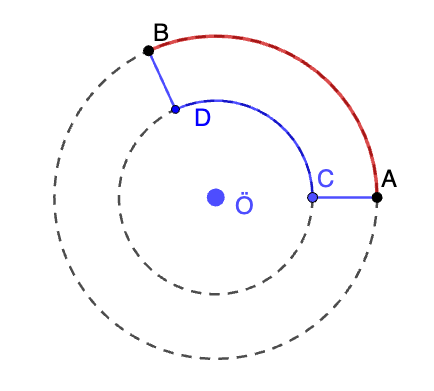
Ongelma 2. Muodostetaan kaksi saman keskistä ympyrää. Olkoon ympyröiden keskipiste on Ö, säteet r ja r + d sekä A ja B pisteitä isommalla ympyrällä. Piste C on säteen ÖA ja pienemmän ympyrän leikkauspiste. Piste D säteen ÖB ja pienemmän ympyrän leikkauspiste. Pisteestä A voi kulkea kahta reittiä pisteeseen B, joko ulompaa reittiä eli  ympyrän kaarta AB pitkin tai sisempää reittiä jana AC, ympyrän kaari CD, jana DB. Kuinka suuri kulman AÖB tulee olla, jotta reittien pituudet ovat yhtä suuret. Anna vastaus radiaaneissa.

Ongelma 3. Muutetaan ongelmaa. Ulompi reitti on edelleen ympyrän kaari AB vastapäivään. Muutetaan sisempi reitti niin, että ympyrän kaari CD onkin myötäpäivään. Kuinka suuri kulman AÖB tulee olla, jotta reittien pituudet ovat yhtä suuret?

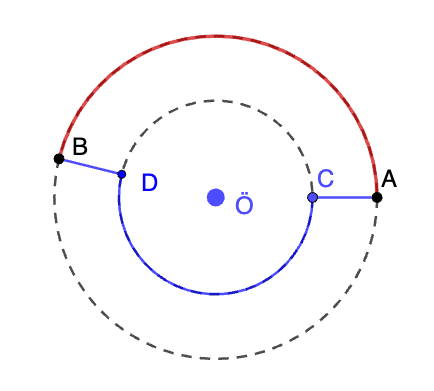
Ongelma 4. Kuinka suuri suhde d/r voi olla, jotta ongelmalle 3 on mielekäs ratkaisu, eli kulma AÖB on positiivinen eikä ylitä täyttä ympyrää.

lähteet

Ülesanne nr. 379
A. Levin, M. Levin. Matemaatika ülesannete kogu keskkoolile. Tln. Valgus 1969. 

Väike-Õismäe Tiik Google Mapsissä
https://www.google.com/maps/place/V%C3%A4ike-%C3%95ism%C3%A4e+pond/@59.4154121,24.6437017,1824m/data=!3m1!1e3!4m6!3m5!1s0x46929449c9677ec5:0x6a8ac3c269d0271a!8m2!3d59.4154275!4d24.6465652!16s%2Fg%2F11bxb8tbv4?hl=en&entry=ttu&g_ep=EgoyMDI1MDMxOS4yIKXMDSoJLDEwMjExNDUzSAFQAw%3D%3D