Tämän kevään pitkän matikan ylioppilaskoetehtävässä 11 pohdittiin kuinka monta nollaa on suuressa luvussa 2000! – 10³⁰⁰. Tässä pohdiskelen, miten selvittää Abittissa olevien ohjelmien avulla, kuinka monta nollaa on luvun 2000! lopussa.

Ensin pitäisi saada aikaiseksi 2000! desimaalilukuna. Geogebra 6:n CAS antaa yhden ratkaisun. Texas Nspire ja Casio Classpad eivät tuottaneet noin suurta lukua numeroina, ainakaan minun taidoillani. Luvun saa laskettua myös Pythonilla, palaan siihen hetken kuluttua.

GeoGebrasta kopioimalla saa luvun vaikkapa LibreOfficen tekstidokumenttiin.

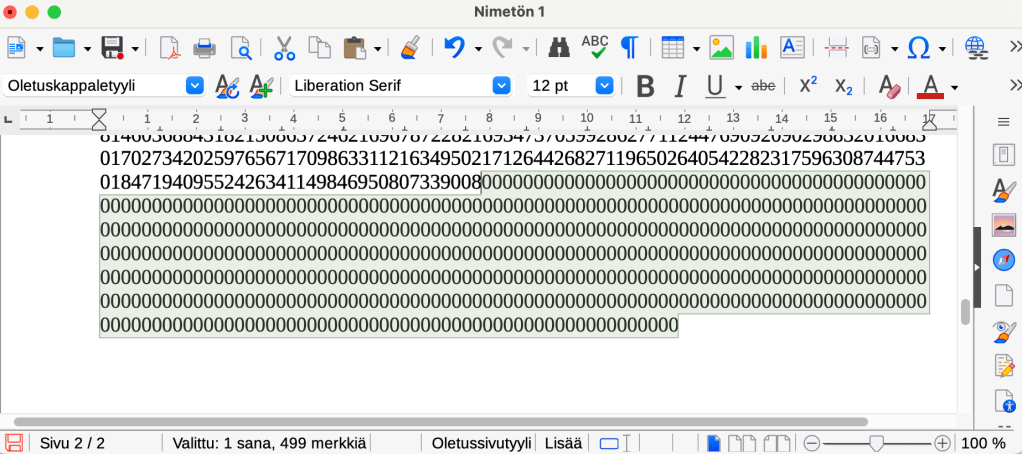
Tuosta on helppo laskea yksi kerrallaan, että nollia lopussa on 499.  Toisaalta kun valitsee lopun nollat, niin LibreOfficen ala-palkissa näkyy valittujen merkkien lukumäärä 499. 

Myös Pythonilla voi laskea nollien lukumäärän tulkitsemalla luvun desimaaliesitys merkkijonona. Käytän seuraavassa Python ohjelmointiympäristönä Abittin Abicodea.

Pythonissa kertoma löytyy math-moduulista. Kun suorittaa seuraavan koodin tulee virheilmoitus.

Luvun desimaaliesitys on liian pitkä tässä Pythonin versiossa. Tämän voi kiertää lisäämällä pisimmän merkkijonon pituutta. 

Nollien määrän lopussa saa laskettua vaikkapa seuraavalla tavalla. Muutetaan luku merkkijonoksi ja lasketaan sen pituus. Poistetaan nollat ja lasketaan tämän merkkijonon pituus. Vähentämällä pituudet toisistaan saadaan lopussa olevien nollien lukumäärä. 

Alla on ensin esimerkki, joka osoittaa, että koodi toimii niinkuin pitääkin. Koodin rivillä 14 poistetaan nollat rstrip-metodilla.

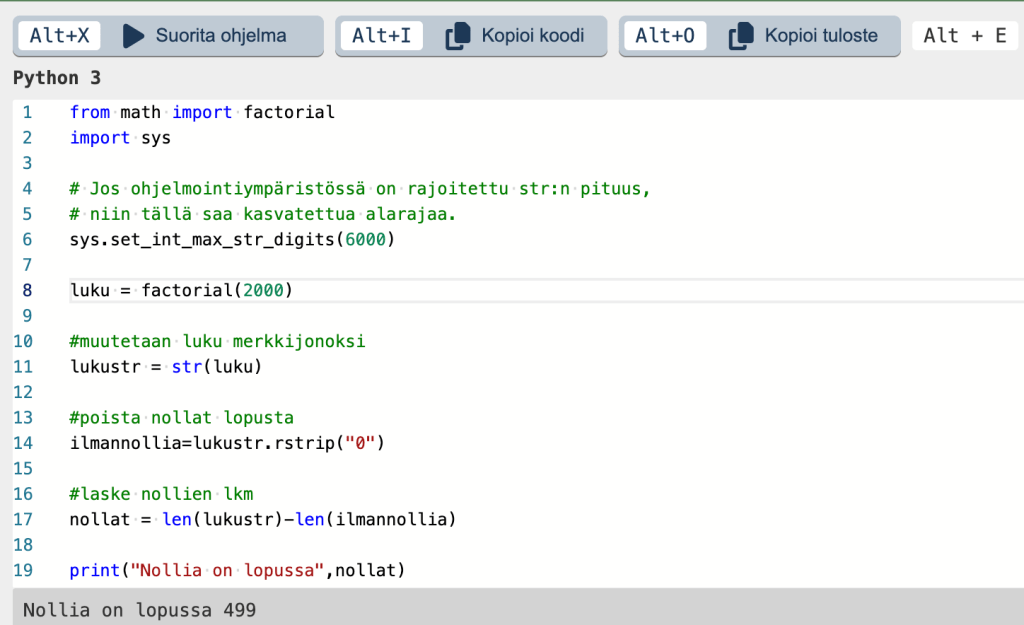
Tässä vaiheessa ei ole tarvittu kuin kertolaskua ja vähennyslaskua nollien lukumäärän laskemiseksi. Tutkitaan, miten nollien määrä kasvaa kertomien lopussa. Loin edelliseen koodiin perustuvan funktion, jonka avulla laskin luvun kertoman lopussa olevien nollien lukumäärän. Selvästi nollien määrä muuttuu viidellä jaollisten lukujen kohdalla

Uudessa taulukossa on vain joka viides luku.

Nollien lukumäärä kasvaa yhdellä, paitsi niissä viidellä jaollisissa luvuissa, joissa tekijänä on useampia viitosia.

Kun ongelmaa pohtii hieman aikaa, niin ymmärtää, että luvun N! lopussa olevien nollien lukumäärä on yhtä suuri kuin luvun N! tekijöissä olevien viitosten lukumäärä.

Jos tämän haluaa laskea Pythonilla, niin tekijöihin jako löytyisi esimerkiksi PrimePy moduulista. Se ei ole käytettävissä Abicodessa. Pitää tehdä itse algoritmi, joka laskee luvu N! tekijöissä olevien viitosten lukumäärän.

Alla olevassa koodissa käydään kaikki viidellä jaolliset luvut riviltä 3 alkavassa for-silmukassa. Viidellä jaollisuus testataan rivin 5 while-komennon ehtolauseessa.

Toki tuon viitosten lukumäärän tekijöissä olisi saanut selvitettyä GeoGebran tekijöihin jaon avulla. JaaTekijöihin() -komento esittää luvun tekijät perinteisesti potensseina ja Tekijät() -komento matriisina.

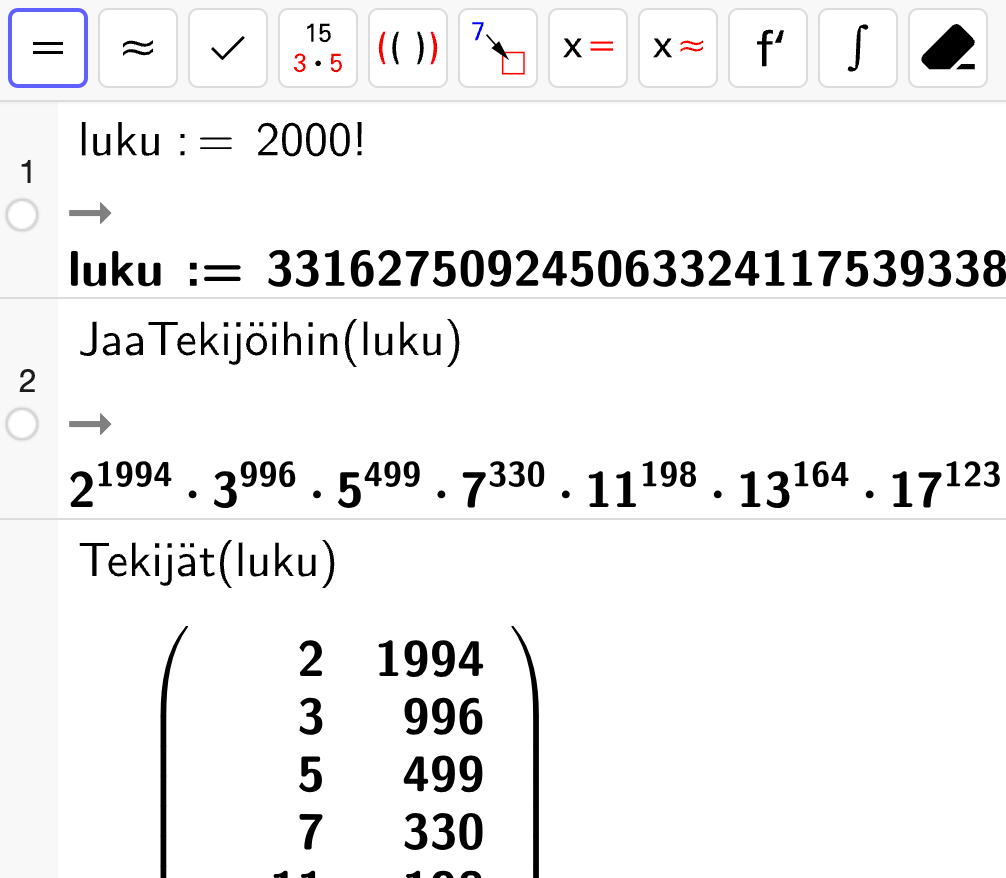
Ongelma 1. Kevään 2025 pitkän matikan Hyvän vastauksen piirteet -dokumentissa on esitetty kaava luvun 2000! lopussa olevien nollien lukumäärälle. 

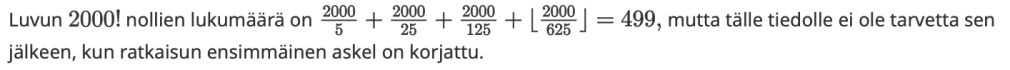
Luo yleinen kaava, jonka avulla voi laskea luvun N! lopussa olevien nollien lukumäärän.

Ongelma 2. Kuinka monta nollaa on luvun 20000! lopussa?

Ongelma 3. Luku 2000! on suuri. GeoGebran mukaan sen likiarvo on noin

Miten muutat Pythonilla luvun factorial(2000) tai factorial(20000) arvon kymmenpotenssimuotoon? 

lähteet

Abicode
https://abicode.abitti.fi

Kevään 2025 pitkän matikan yo-tehtävä 11
https://yle.fi/plus/abitreenit/2025/kevat/matematiikka_pitka/index.html#question-nr-11

Kevään 2025 pitkän matikan HVP
https://yle.fi/plus/abitreenit/2025/kevat/matematiikka_pitka/hvp_lopullinen.pdf