[edit. 30.8.25. korjasin muutaman kirjoitusvirheen.]

Edellisessä artikkelissani esitin neljä lausetta, jotka liittyivät kolmion sisään ja ulkopuolelle piirrettyjen monikulmioiden aloihin. Esitän tässä lauseille todistukset. Kerron myös, miten käytin apuna GeoGebra CAS:ia. Tämä on aika pitkä tarina :o)

Alun perin tein laskuni GeoGebra 5:llä, koska sen avulla pystyn ratkomaan ongelmia sutjakkaammin. Esitän tässä ratkaisun GeoGebra Classic 5:n ja 6:n avulla.

Käytän tässä erikoistapauksena kolmiota, jossa on pisteet A = (0, 0), B=(1, 0) ja C =(0, 1). Geometrian ymmärtämykseni mukaan affiineissa kuvauksissa janojen pituuksien väliset suhteet eivät muutu, niinpä erilaiset kierrot, siirrot  ja venytykset eivät muuta laskettujen pinta-alojen suhteita. Tarinan lopussa esitän vielä yleisemmän ratkaisun, missä C pisteet koordinaatit ovat (a, b).

 Edellisessä artikkelissani merkitsin suhdelukumuuttujaa u-kirjaimella. Kun loin todistuksia CAS:issa vaihtui kirjain vahingossa e:ksi.

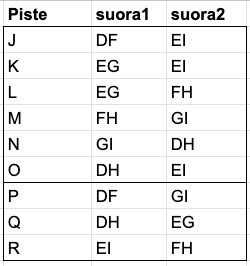
pisteiden koordinaatit

Luodaan kolmio ABC. Tässä tietysti A, B ja C eivät ole samalla suoralla. Olkoon e luku väliltä ]0, 1/2[. Pisteet D ja E jakavat janan AB suhteessa e : 1 – 2 e : e. Nyt janat AD/AB  = BE/AB = e. Vastaavasti pisteet F ja G jakavat janan BC sekä pisteet H ja I jakavat janan CA samassa suhteessa.

Tällöin pisteiden D, F, …, I koordinaatit ovat:

Pisteet J, …, R ovat taulukossa näkyvien suorien leikkauspisteissä.

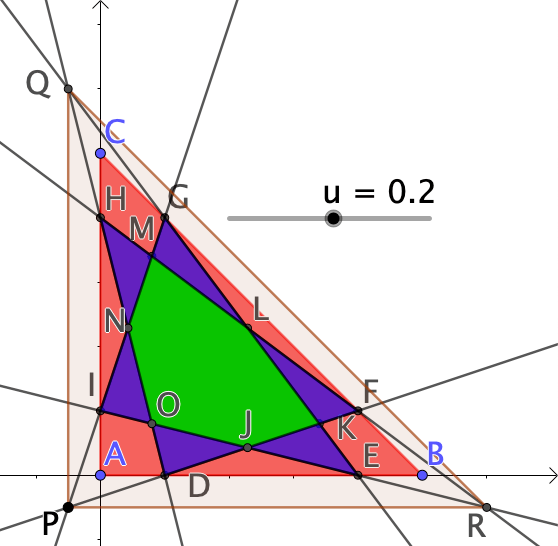
Edellisen reseptin mukainen kuva.

lause 1

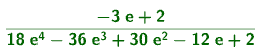
Todistus

Määritin GeoGebran CAS:issa pisteiden J, …, O koordinaatit. Koska Leikkauspiste(suora1, suora2) tulostaa listan tyyliin {(x1, y1), (x2, y2), …} sain pelkän pisteen käyttöön käyttämällä Alkio(lista, mones)-komennon apuna. Alla pari esimerkkiä.

Samalla tavalla sain muut pisteet. Tavoitteena oli laittaa pisteet kuusikulmion pisteet J, …, O listaan, jonka avulla olisin saanut alan laskettua käyttämällä Shoelace-kaavaa. Tässä tuli ongelma, sillä GeoGebran Classic 5 ja 6 versiot ymmärtävät pisteen, joissa on muuttujia, kompleksitason pisteiksi.  Katso liitteessä oleva linkki GeoGebra foorumin keskustelusta.  Minun piti muuttaa pisteet listaksi käsin tyyliin

jne.

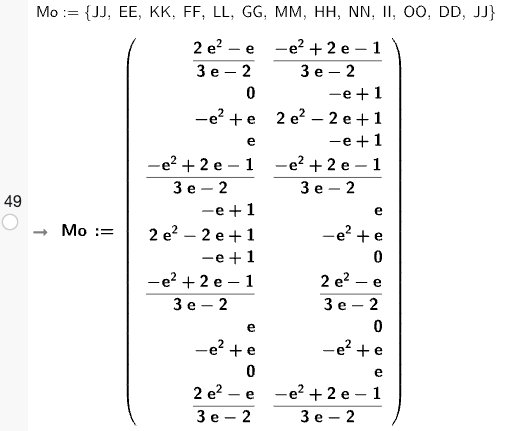
Seuraavaksi loin listan Mo.

Mo onkin itse asiassa matriisi. Matriisissa alkion saa tulosteeksi Alkio(Rivi, Sarake)-komennolla. Esimerkkinä neljännen rivin ja toisen sarakkeen alkion arvo.

Käytin pinta-alan laskemiseen Kengännauha(Shoelace)-kaavaa, siksi Mo matriisissa pitää olla monikulmion ensimmäinen piste myös viimeisenä.

Summa-komennolla kuusikulmion alaksi saadaan e:n funktiona:

h(e):=((1)/(2))*Summa( Alkio(Mo, n, 1)*Alkio(Mo, n+1, 2)-Alkio(Mo, n+1, 1)*Alkio(Mo, n, 2), n, 1, Pituus(Mo)-1)

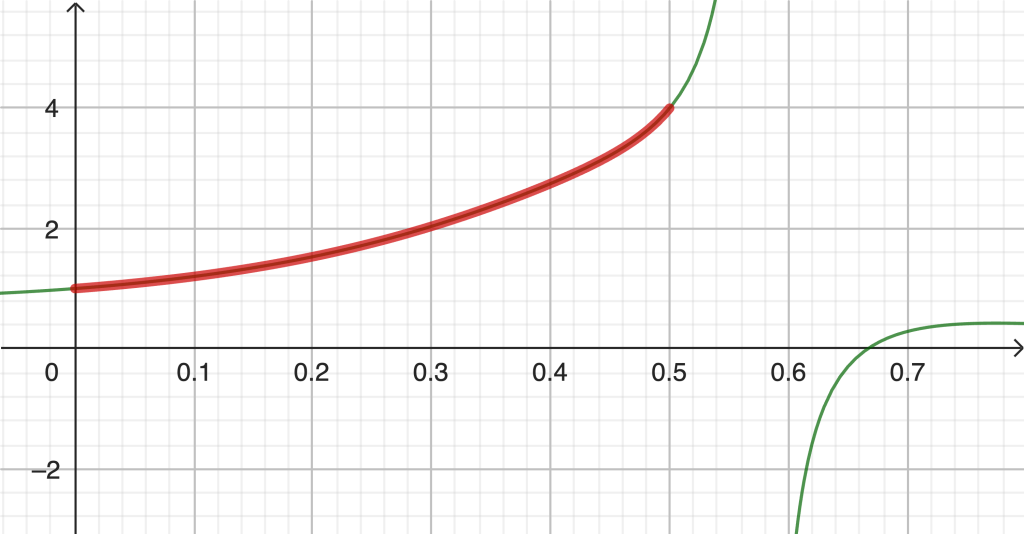
Tosin tuo edellinen on miinusmerkkinen. Niinpä alojen suhteeksi saadaan sievennettynä

kun 0<e<½. Piste P = (⅓, 9/2) ja musta piste ääriarvopiste.

Suurin arvo on

Tämä todistus on periaatteessa sama kuin mitä ChatGPT tarjosi, kun pyysin siltä todistusta. Muut käyttämäni tekoälyt Gemini ja Copilot eivät ratkaisseet ongelmaa oikein. Alla ChatGPT:n ratkaisun loppu

lause 2

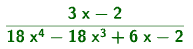
Todistus

Nyt kun minulla oli valmis ratkaisu monikulmioiden alojen laskemiseen, oli helppoa vain vaihtaa Mo listaan pisteet. Tämän tehtävä ratkaisussa ChatGPT teki joitain kummallisia virheitä. 

lause 3

Kolmion ABC ja kuusikulmion DEFGHI alojen suhde on vakio.

Todistus

Samalla tavalla.

lause 4 todistus

Kolmioiden ABC ja PQR alojen suhde on vakio. 

Todistus

Tässä e voi saada mitä tahansa reaaliarvoja, jopa miinusmerkkiset toimivat.

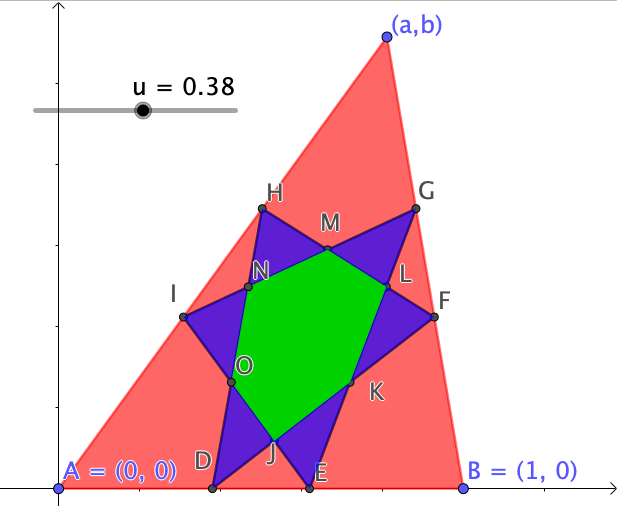
QED

yleisempi tapaus

Ensimmäistä todistusta tehdessäni pohdin mitä tapahtuu pisteen B koordinaateille todistuksessa. Niinpä päätin luoda yleisemmän todistuksen, jossa pisteen C koordinaatit (a, b). Toisaalta tämä toimi myös tarkistuksena alkuperäisille todistuksille.

Alla CAS-todistuksen alkua.

Pistematriisi on hieman monimutkaisempi kuin erikoistapauksessa. Pisteiden koordinaateissa on mukana a ja b.

Alan lausekkeesta a:n arvo katoaa.

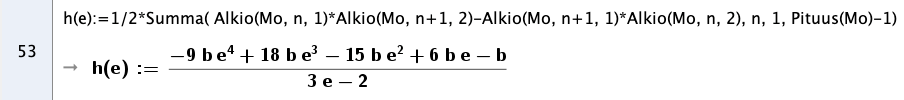
Suhteen lausekkeesta myös b supistuu pois, niin kuin pitääkin ja saadaan sama tulos kuin alkuperäisessä todistuksessa.

---

Lisään todistuksissa käytetyt tiedostot GeoGebra Materiaaleihin GG-kirjaksi.

---

lähteet

Mikon kuusikulmio kolmiossa lauseet
https://mikkorahikka.blog/2025/08/21/mikon-kuusikulmio-kolmiossa-lauseet/

Mikko’s theorems on heksagram in triangle GeoGebra Materiaaleissa
https://www.geogebra.org/m/habevzue

Shoelace formula Wikipediassa
https://en.wikipedia.org/wiki/Shoelace_formula

Problem with points with parameters in CAS GeoGebra Reddit-foorumilla
https://www.reddit.com/r/geogebra/comments/1n1bem9/problem_with_points_with_parameters_in_cas/

CAS-todistukset monikulmiot kolmiossa -lauseille GeoGebra-kirja GG Materiaaleissa
https://www.geogebra.org/m/wxgwrqwg