Laskeskelin GeoGebran avustuksella laskuja murtoluvuilla. Välillä GeoGebra supisti murtolukuni ja välillä ei. Aloinpa pohdiskella kuinka yleistä on, että satunnainen murtoluku sievenee tai ei sievene yksinkertaisemmaksi.
Tein pienen animaation, jossa a:lla on arvo 24 ja b saa arvot 1, …, 50. Toisinaan murtoluku supistuu, toisinaan taas ei.
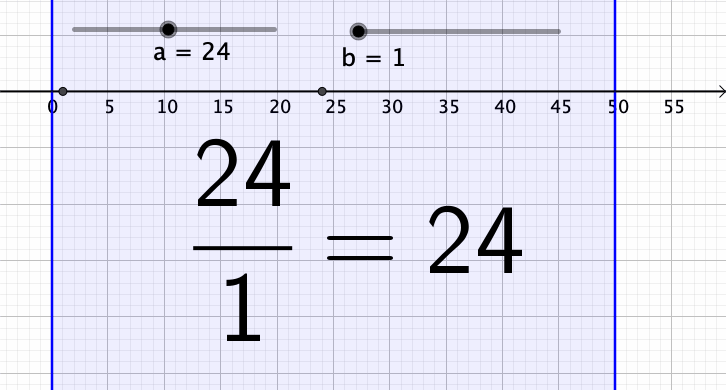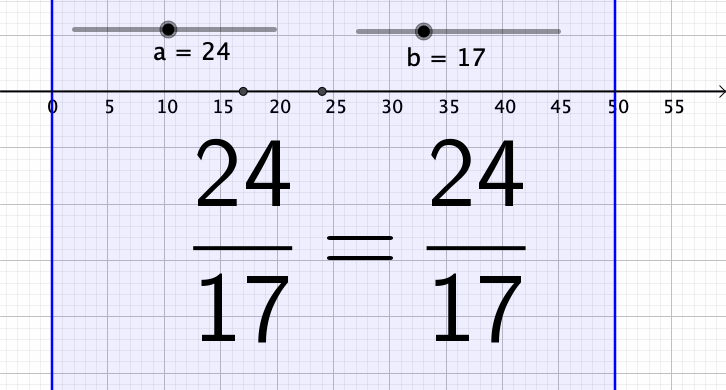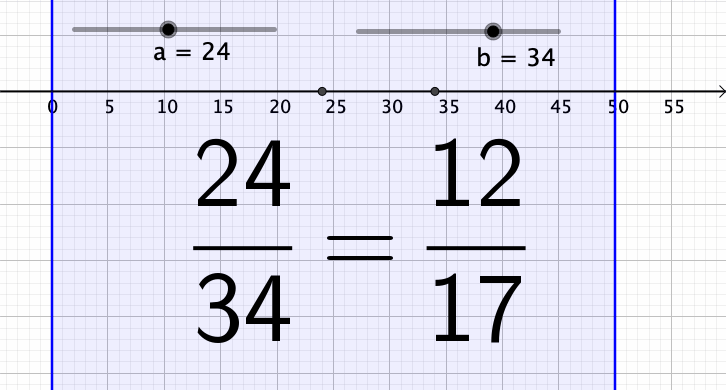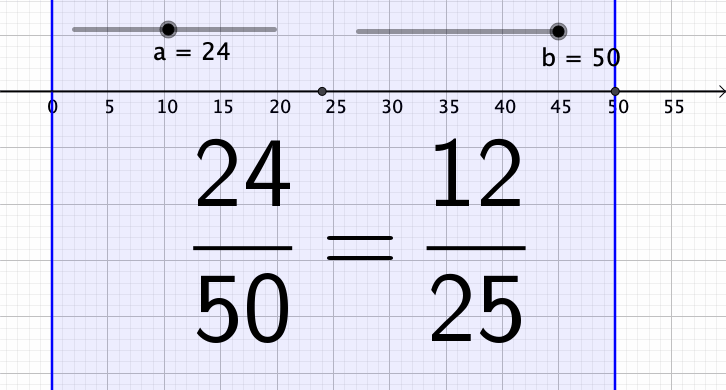
Murtoluku a/b:n voidaan supistaa, jos luvuilla a ja b on yhteisiä tekijöitä. Jos murtolukua a/b ei voi supistaa, niin silloin a:lla ja b:llä ei ole yhteisiä tekijöitä ja tällöin niiden suurin yhteinen tekijä on 1. Englannin kielellä tällaiset luvut ovat coprime.
Esimerkiksi luvuilla 15 = 3*5 ja 28 = 4*7 ei ole yhteisiä tekijöitä, niinpä GeoGebran CAS:issa
SYT(15, 28) = 1
tai Pythonissa math-moduulin avustuksella

Piirsin GeoGebralla pisteitä koordinaatistoon, jos a:lla ja b:llä ei ole yhteisiä tekijöitä. Tässä yhteydessä laskin kuinka suurella osuudella lukupareista (a, b) ei ole yhteisiä tekijöitä, kun a ja b saavat pareittain kaikki arvot välillä 1, 2, …, N. GeoGebra-kuvissa tämä luku on merkitty f:llä. Sovitaan, että alamme tutkia funktiota f(N), jonka arvo on kyseinen suhde. Niinpä alemman kuvan perusteella f(10) = 0.63 ja seuraavien kuvien perusteella f (50) ≈ 0,6188, f(100) ≈ 0,6087.

kuva 50

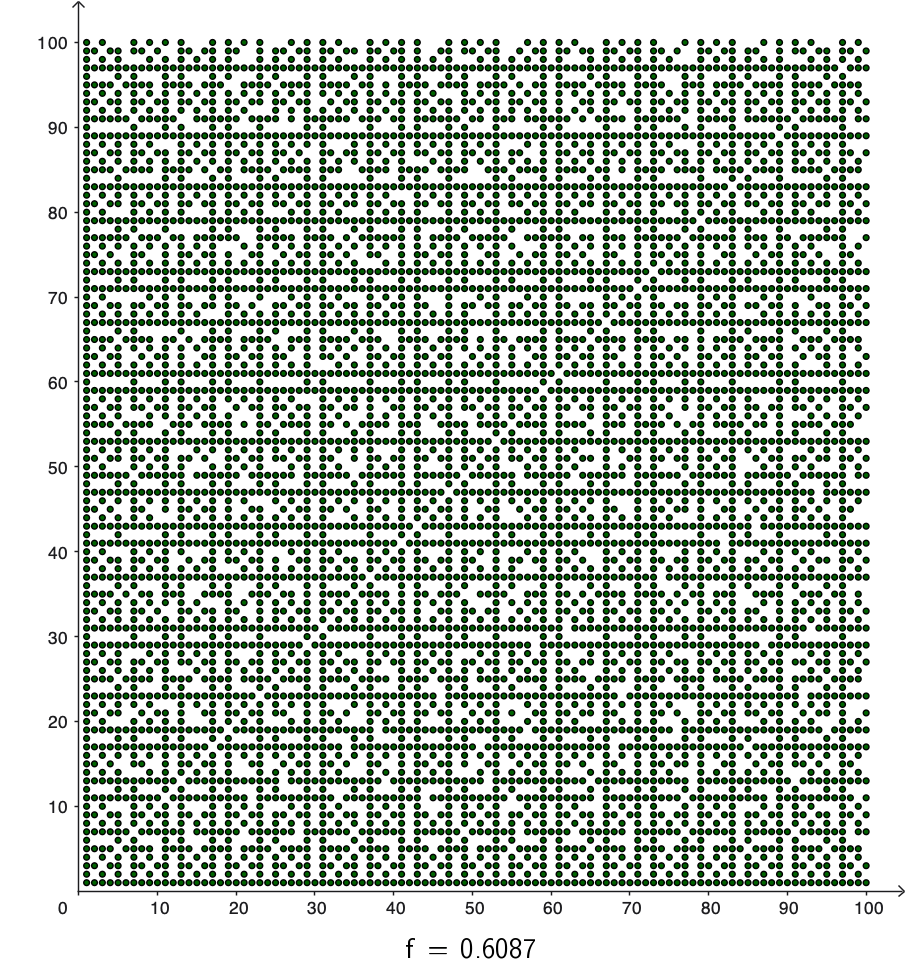
Viimeistään tässä vaiheessa huomaa, että pisteiden tiheys pysyy lähes samana vaikka vaikka N:n arvo kasvaakin.
kuva 300
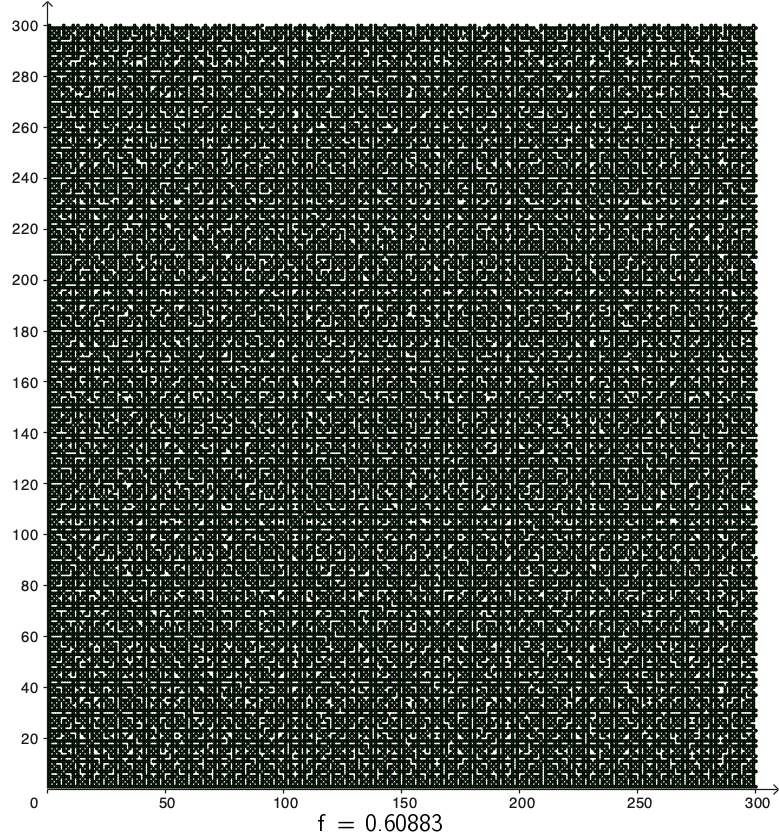
Tässä vaiheessa GeoGebran pienimmän pisteen koko alkoi rajoittaa kuvien tutkiskelua. Toisaalta N:n kasvattaminen sai aikaan laskenta-ajan kasvamisen epämiellyttävän pitkäksi, GeoGebra kun ei ole kovin nopea laskija.
Koodasin Pythonilla pienen ohjelman pätkän, jonka avulla ilmiötä voi tutkiskella. Myös N:n arvolla 500 näyttää siltä, että pisteiden jakauma on melkoisen tasainen.

Mitä tapahtuu f:n arvolle, kun n kasvaa? Alla Pythonilla laskettuja f(n):n arvoja.

Lukuteoria kertoo meille, että

Ongelma 1. Todista, että jos valitaan kaksi satunnaista lukua, niin todennäköisyys, että luvuilla ei ole yhteisiä tekijöitä on
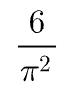
Ongelma 2. Mitä jos otetaan kolme satunnaista luonnollista lukua. Kuinka suuri on tällöin todennäköisyys, että niillä ei ole pareittain yhteisiä tekijöitä?
Palaan tähän aiheeseen seuraavassa tarinassani. Siinä pohdiskelen kuvaajissa näkyviä hahmoja.
lähteet
Coprime Wikipediassa
https://en.wikipedia.org/wiki/Coprime_integers
Keskenään jaottomat luvut Wikipediassa
https://fi.wikipedia.org/wiki/Kesken%C3%A4%C3%A4n_jaottomat_luvut

Jätä kommentti