Vuosi vaihtui ja saimme uuden vuosiluvun. Tutkitaan joitakin lukuun 2026 liittyviä kummallisuuksia tai itsestäänselvyyksiä. Keskityn tässä lukuun 1/2026 jaksollisena desimaalilukuna ja yhtälöiden x2 + y2 = 20262 ja x2 + y2 + z2 = 20262 kokonaislukuratkaisuihin.
Luvun 2026 alkutekijät ovat 2 ja 1013. Niinpä 10132 + 10132 + 10132 + 10132 = 20262. Geometrinen todistus edelliseen totuuteen on seuraavassa kuvassa.
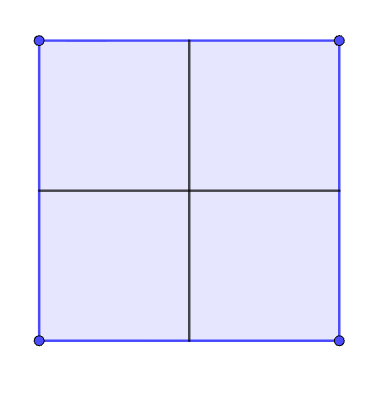
1/2026 desimaalilukuna
Luvun 1/2026 desimaalikehitelmä on jaksollinen, sen jakso on suhteellisen pitkä, 253 desimaalia. Alla olevassa likiarvossa on 260 desimaalia.
1/ 2026 ≈ 0.00049358341559723593287265547877591312931885488647581441263573543928923988153998025666337611056268509378084896347482724580454096742349457058242843040473840078973346495557749259624876604146100691016781836130306021717670286278381046396841066140177690029615004935
Tutkitaan lukua a = 4935834155972359328726554787759131293188548864758144126357354392892398815399802566633761105626850937808489634748272458045409674234945705824284304047384007897334649555774925962487660414610069101678183613030602171767028627838104639684106614017769002961500 eli otetaan luvun 1/2026 desimaalikehitelmän jakso siten että alkunollat ovat lopussa. Tällöin
1/a ≈ 2.0260·10253 ≈ 0.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000020260000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000002026…
Jälkimmäinen likiarvo on esitetty 509 desimaalin tarkkuudella, sen avulla huomannee, että 1/a:n desimaaliesityksen jakson pituus on myös 253 numeroa.
Sama ilmiö näkyy joillakin pienemmilläkin luvuilla. Luku 1/7 ≈ 0.142857142857…. Jakso on 142857 ja 1/142857 ≈ 0.00000700000700000…
Toisaalta 1/9 ≈ 0,111111…, mutta 1/1 =1. Toisaalta 1/11 ≈ 0,09090…. eli sellaisilla luvuilla, joilla jakso on yhden numeron mittainen, pitää ottaa jaksoksi kaksi numeroa (paitsi kolmosen tapauksessa, mutta se onkin eri juttu). Myös 1 / 6 ≈ 0.1666… on ongelmallinen. Jakso on 6, mutta ennen sitä on tuo ykkönen. Sekään ei kelpaa tutkittavaan tapaukseen.
Oheiseen taulukkoon olen kerännyt sellaisia 25 pienempiä lukuja, joilla jakson käänteislukuilmiö näkyy. Otin mukaan vain sellaiset luvut, joilla jakson pituus on suurempi kuin kaksi. Jakso muutetaan luonnolliseksi luvuksi siten, että jakson alkunollat siirretään luvun loppuun.
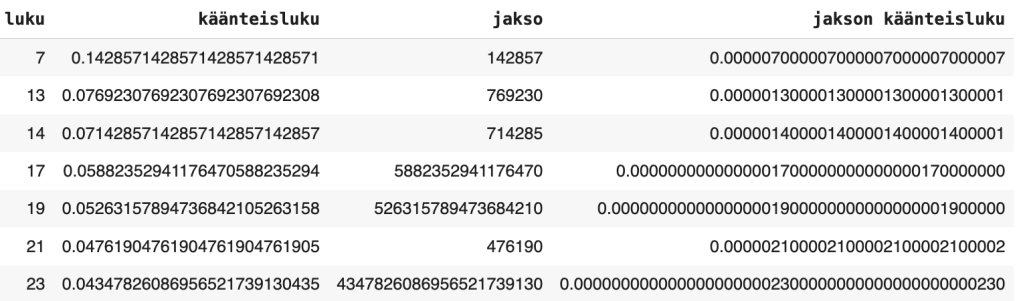
Ongelma 1. Tutki edellistä taulukkoa ja luo matematiikan väite, joka kuvaa edellä esitetyn matemaattisen ilmiön. Todista väitteesi. Tai anna esimerkki jostain luvusta, jolla väitteesi ei pidä paikkaansa.
Kun tutkitaan edellisessä taulukossa käänteislukujen desimaaliesitysten jaksojen pituutta, niin havaitaan että jaksot ovat yhtä pitkät.
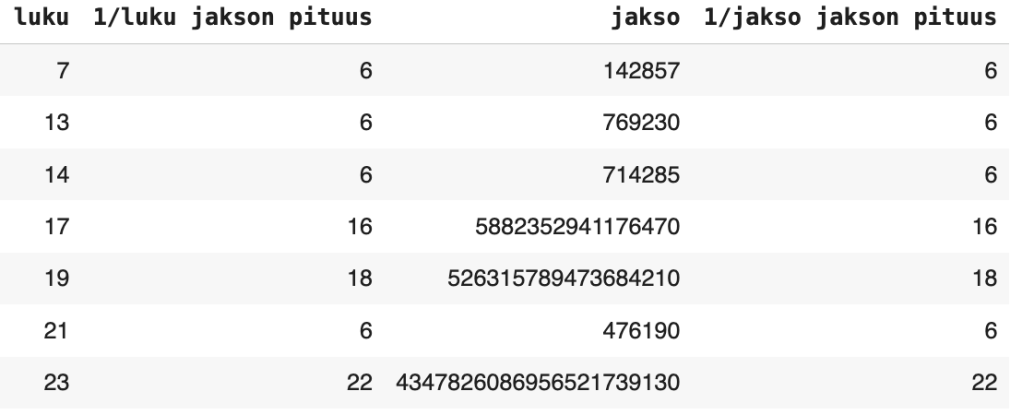
Ongelma 2. Todista, että luvun käänteisluvun ja jakson käänteisluvun desimaalikehitelmien jaksojen (luonnollisina lukuina ja jakson alkunollat siirretään loppuun) käänteislukujen desimaalikehitelmien jaksojen pituudet ovat yhtä pitkiä, mikäli jakson pituus on vähintään kolme. Tuo edellinen virke on ihan mahdoton ymmärtää, toivottavasti se on oikein :o) Tai anna esimerkki jostain luvusta, jolla väite ei pidä paikkaansa.
Yritetään määritellä väite toisella tavalla. Olkoon f(n) luonnollisen luvun n käänteisluvun 1/n jakso esitettynä luonnollisena lukuna siten, että alkunollat on siirretty luvun loppuun. Tällöin f(n):n ja f(f(n)):n numeroiden lukumäärät ovat yhtä suuret, mikäli f(n) on pituudeltaan vähintään kolme.
1/1013
Kun leikin desimaalien jaksoilla huomasi vielä yhden kummajaisen. Luku 1013 on luvun 2026 alkutekijä, päätinpä tutkiskella luvun 1/1013 desimaalikehitelmää.
1/ 1013 ≈ 0.00098716683119447186574531095755182625863770977295162882527147087857847976307996051332675222112537018756169792694965449160908193484698914116485686080947680157946692991115498519249753208292201382033563672260612043435340572556762092793682132280355380059230009871668
Jakso on b = 9871668311944718657453109575518262586377097729516288252714708785784797630799605133267522211253701875616979269496544916090819348469891411648568608094768015794669299111549851924975320829220138203356367226061204343534057255676209279368213228035538005923000, sen pituus on 253 eli sama kuin luvun 1/2026 desimaalikehitelmän jakson pituus. Aiemmin merkittiin 1/1026:n jaksoa a:lla.
Kun laskin Pythonissa

Minua kummastuttaa miksi b = 2a.
Pythagoraan kolmikot ja nelikot
Pythagoraan kolmikot (yhtälön x2 + y2 = n2 positiiviset kokonaislukuratkaisut) voi tulkita suorakulmaisiksi kolmioiksi, joissa kateettien pituudet ovat x ja y ja hypotenuusa on n. Jos ratkaisuksi hyväksytään kaikki kokonaisluvut, niin ratkaisut asettuvat n-säteisen ympyrän kaarelle. Toki kolmikot voisi tulkita myös suorakaiteiksi, joiden sivujen pituudet ovat x ja y, n on tällöin suorakaiteen lävistäjä.
Yhtälön x2 + y2 = 20262 aidosti positiiviset ratkaisut ovat x = 90 ja y = 2024 sekä x = 2024 ja y = 90. Viime vuoden yhtälössä niitä oli 4.
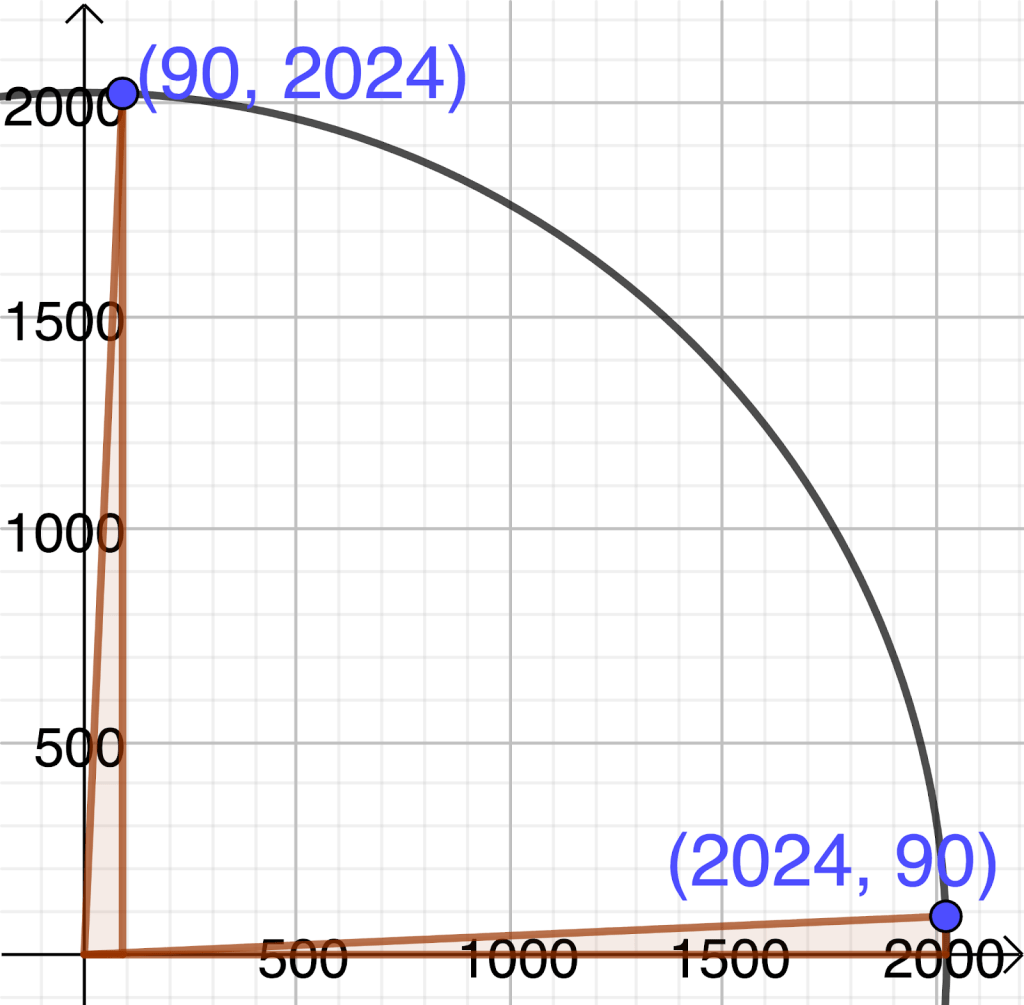
Yhtälöllä on x2 + y2 + z2 = 20262 on 6078 kokonaislukuratkaisua. Ne asettuvat 2026 säteisen pallon pinnalle. Mikäli lasketaan vain ne ratkaisut, joilla x, y, ja z > 0, niin ratkaisuja on 756.
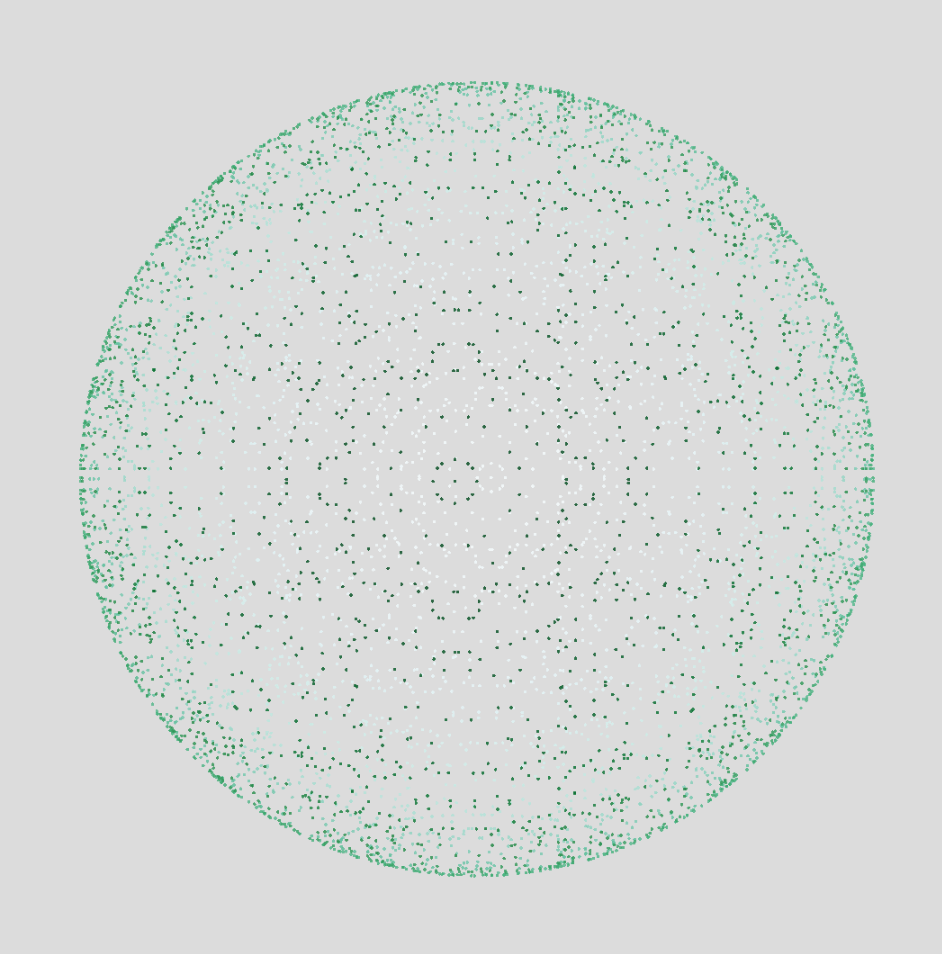
Laskeskelin, mikä on tilavuudeltaan suurin suorakulmainen särmiö, jonka yksi kärki on origossa ja diagonaalisesti vastakkainen kärki kokonaislukuratkaisupisteessä. Sain suurimmaksi tilavuudeksi 1591826688.
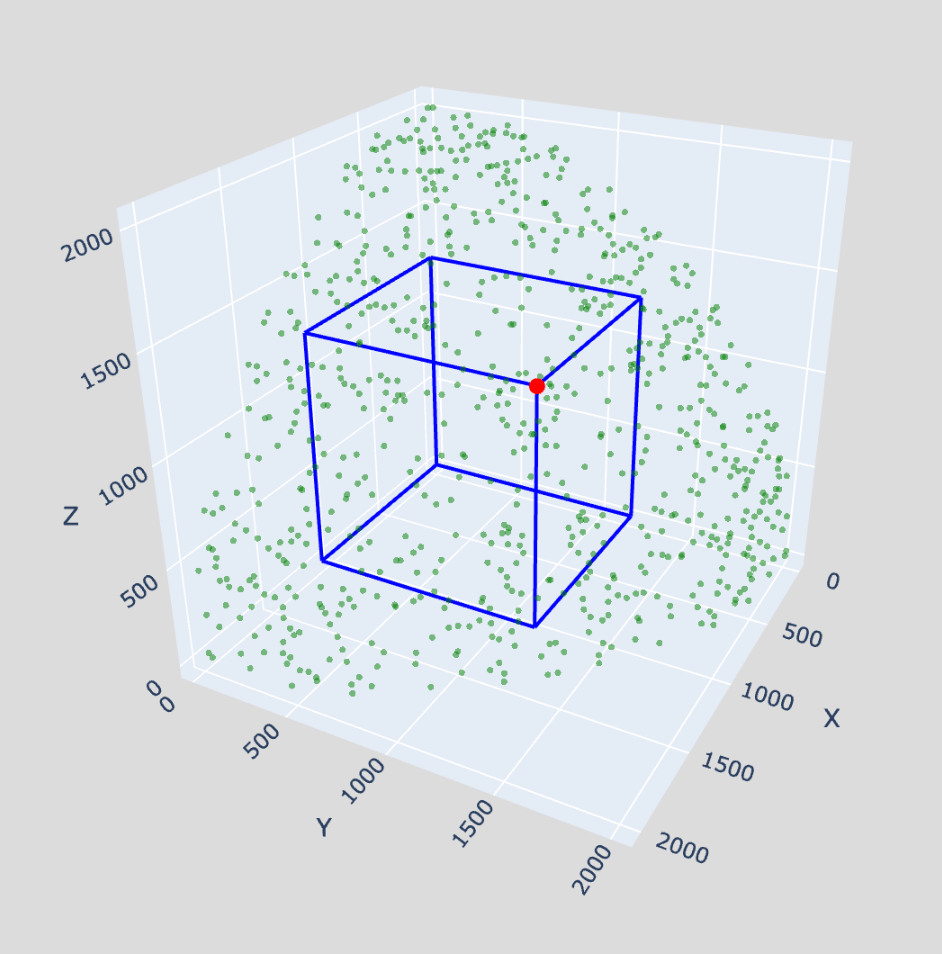
Ongelma 3. Missä pisteessä (pisteissä) on edellä kuvatun särmiön se kärkipiste, joka on yhtälön x2 + y2 + z2 = 20262 kokonaislukuratkaisu. Kuvan punainen piste. Särmiön tilavuus on 1591826688.
Viime vuonna laskin (taisi jäädä julkaisematta), mikä on tilavuudeltaan suurin sellainen neliöpohjainen suorakulmainen särmiö, jonka pohjaneliö on xy-tasossa ja muut kärjet kokonaislukupisteissä x2 + y2 + z2 = 20252. Silloin sain ratkaisuksi pisteen (900, 900, 1575).
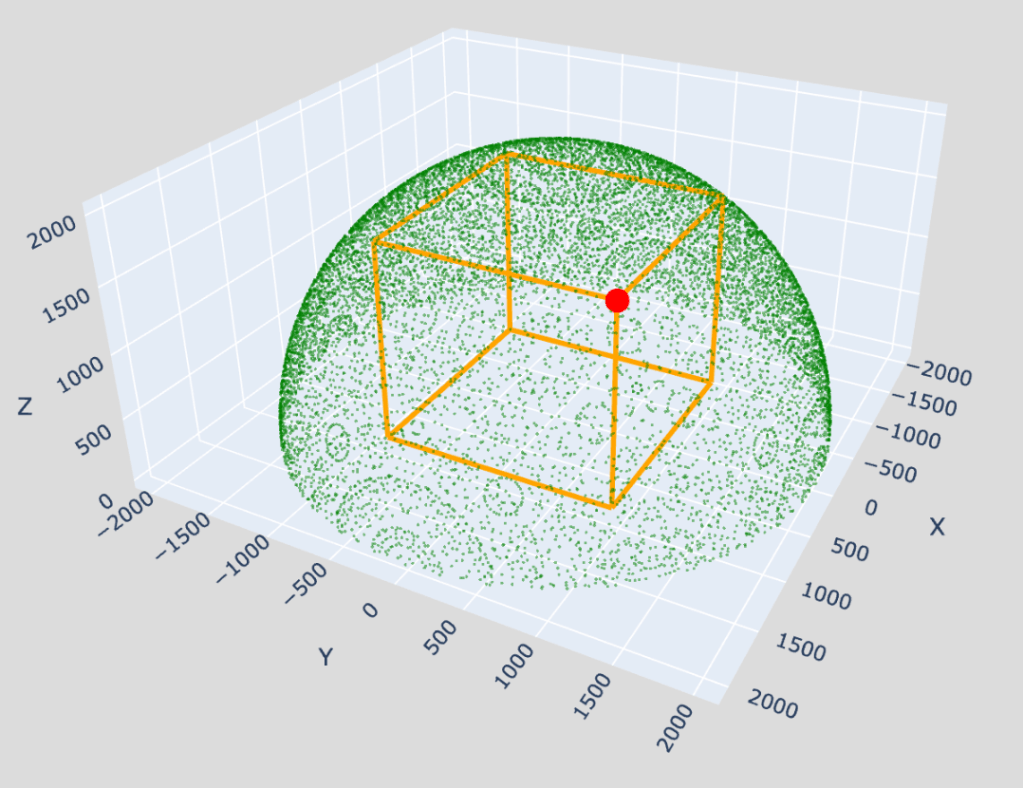
Kun laskeskelin Python-koodini avulla samaa yhtälöllä x2 + y2 + z2 = 20262, niin yhtään ratkaisua ei löytynyt.
Ongelma 5. Todista, että yhtälön x2 + y2 + z2 = 20262 kokonaislukuratkaisuista ei voi valita pistettä (a, a, c), että se olisi sellaisen neliöpohjaisen suorakulmaisen särmiön kärkipiste, jonka pohjaneliön kärjet ovat pisteissä (±a, ±a, 0).
lähteet
Yksikkömurtolukujen desimaalikehitelmien jakson pituuksista 1 – pohdittavaa, ongelmia
https://mikkorahikka.blog/2022/09/20/yksikkomurtolukujen-desimaalikehitelmien-jakson-pituuksista-1-pohdittavaa-ongelmia/
Yksikkömurtolukujen desimaalikehitelmien jakson pituuksista 2 – jakson pituus Pythonilla
https://mikkorahikka.blog/2022/09/29/yksikkomurtolukujen-desimaalikehitelmien-jakson-pituuksista-2-jakson-pituus-pythonilla/
2025 Pythagoraan kolmikot ja nelikot
https://mikkorahikka.blog/2024/12/31/2025-pythagoraan-kolmikot-ja-nelikot/

Jätä kommentti