Edellisessä artikkelissani esitin ongelman liittyen kolmioiden sivujen pituuksiin. Ongelmassa piti löytää yhteyksiä taulukon kokonaislukupituuksien ja kolmion ominaisuuksien kanssa. Seuraa varoitus, alla oleva paljastaa ratkaisun ongelmaan. Seuraavat ongelmat ratkennevat tekoälyn avulla, niinpä älä käytä tekoälyä ratkaisuissasi.
Lause 1. Olkoon ABC sellainen kolmio, että A:n vastainen sivun pituus on a, B:n b ja C:n c. Olkoon kulma CAB kaksinkertainen verrattuna kulmaan ABC. Tällöin
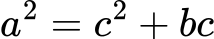
Ongelma 1. Todista Lause 1 käyttäen apuna trigonometriaa.
Ongelma 2. Todista Lause 1 geometrisesti ilman trigonometrisia funktioita.
Kun piirtelin tätä, niin muistuipa mieleeni totuus kolmioista, pitihän sitäkin kokeilla tässä yhteydessä.
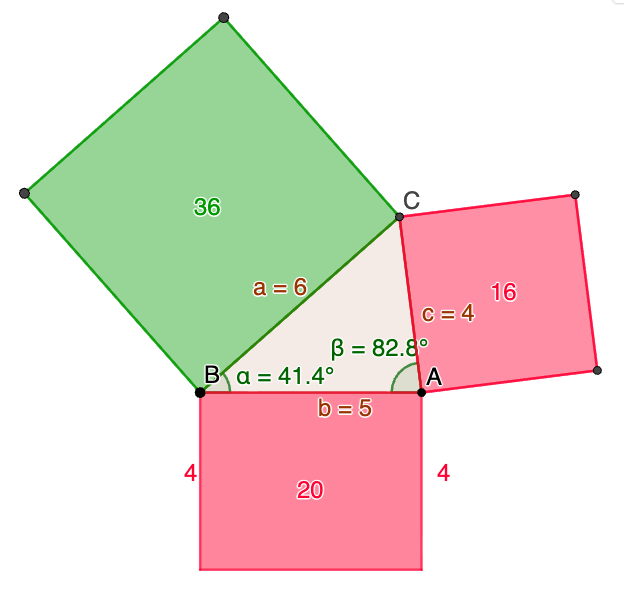
Ongelma 3. Todista, että kolmioissa joissa on kaksinkertainen kulma, harmaat pinta-alat ovat yhtä suuria.
Ongelma 4. Todista, että kolmioissa joissa on kaksinkertainen kulma, punaiset pinta-alat ovat yhtä suuria.
Lisätään vielä yleinen tapaus edellisestä.
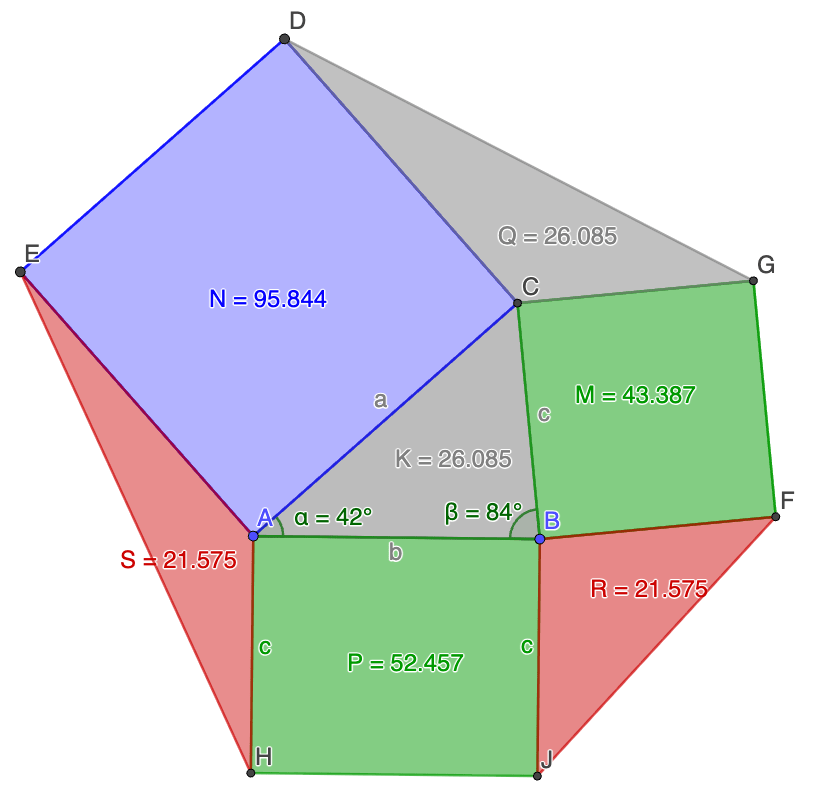
Lause 5. Olkoon ABC kolmio ja piirretään sivuille a, b, ja c suorakulmaiset kolmiot. Muodostetaan kolmiot, joiden kärjet ovat suorakulmaisen kolmion kärki ja kahden suorakulman kärjet, kuten kuvassa. Tällöin kyseisillä kolmella kolmiolla ja alkuperäisellä kolmiolla on sama ala.
yleistys
Mitä jos kolmiossa on kolminkertainen kulma? Minä en saanut aikaiseksi geometrista todistusta, mutta GeoGebra CAS:in, kosinilauseen ja trigonometristen palautuskaavojen avulla sain aikaiseksi tällaisen yhtälön.
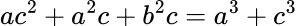
Sitten tietysti alkoi kiinnostamaan, mitä tapahtuu kun toinen kulma on nelinkertainen tai viisinkertainen. Tässä vaiheessa piti hypätä tekoälyn puoleen selvittämään, miten tarina jatkuu.
ChatGPT käyttää yleisessä ratkaisuissa apuna Chebyshevin polynomeja, niinpä jätän aiheen syvällisemmän kommentoinnin minua fiksummille. ChatGPT ottaa kantaa myös yhtälöiden kauneeteen. Minusta nuo kaikki ratkaisut ovat kauniita. Ei yhtälöitä saa syrjiä ulkonäön perusteella.

Tässä vaiheessa tajusin, että 4.asteen ratkaisu on siinä mielessä kummallinen, että se on kolmannen asteen polynomi, kokeillaan Gemijiä.
Geminin ratkaisu tapaukselle B = 4A on
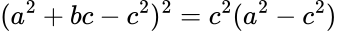
Tämä vaikuttaa fiksummalta, sillä siinä lausekkeet ovat 4. asteen polynomeja. Kun arvasin, että ei tuokaan voi olla oikein, niin kolmannella yrityksellä Gemini tuotti yhtälön
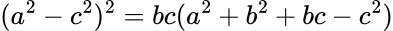
Ongelma 5. Piirrä GeoGebralla tai jollain muulla geometrian piirto-ohjelmalla sellainen kolmio, että A:n vastainen sivun pituus on a, B:n b ja C:n c ja kulma CAB nelinkertainen verrattuna kulmaan ABC. Tarkista, mikä kaavoista on totta, vai onko mikään.
ongelman historiaa
Löysin tämän ongelman alun perin Pat’sBlog:ista. Hän oli löytänyt sen hollantilaisen Arjen Dijksman:nin PHYSICS INTUITIONS -blogista. Arjenin mukaan tämä ongelma on peräisin Leon O. Romainilta. Leonin Usenet artikkeli vuodelta 2002 löytyy Internetin syövereistä.
Pienen salapoliisityö avustuksella havaitsin, että lause on ”keksitty” aiemmin. Konstantin Zelator (2012) käyttää lähteenä vuonna 1976 ilmestynyttä William Wayne Wilsonin artikkelia ”A generalization of the property of the 4,5,6 triangle” Mathematical Gazettessa. Käsitykseni mukaan Lause 1 on todistettu tuossa artikkelissa. Koska minulla ei ole varaa mennä maksumuurin taakse, niin jätän tämä asian selvittelyn niille onnekkaille, joilla on oikeudet Mathematical Gazetten lukuun.
Tuossa Zelatorin artikkelissa osoitetaan, että Lauseen 1 kokonaislukuratkaisut ovat muotoa
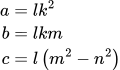
jos m ja k ovat keskenään jaottomia ja k2 < m2 < 2m2.
lähteet
Almost Pythagorean, a collection on a theme Pat’sBlogissa
https://pballew.blogspot.com/2023/01/almost-pythagorean-collection-on-theme.html
Lost theorem about angular proportions PHYSICS INTUITIONS -blogisssa
https://commonsensequantum.blogspot.com/2010/06/lost-theorem-about-angular-proportions.html
The Missing Theorem, Leon O. Romain Usenet-artikkli
https://groups.google.com/g/geometry.research/c/UkLO_iVUJjo?pli=1
Konstantine Zelator. Integral Triangles with one angle twice another, and with the bisector (of the double angle) also of integral length. ArchivX artikkeli
https://arxiv.org/pdf/1208.0497
Chebyshev polynomials
https://en.wikipedia.org/wiki/Chebyshev_polynomials

Jätä kommentti