[edit. 31.10.24 palautin kadonneet kaavat.]

Tällaisen löysin “Miraculous world of Numbers” -blogista. Enpä ole ennen törmännyt tähän. Tästä saa mukavan tutkimus/todistustehtävän peruskoululaisille ja lukiolaisille. 

Tutkitaan tätä ongelmaa GeoGebran CASilla.

Kolmella numerolla

Taulukkolaskennalla sama juttu.

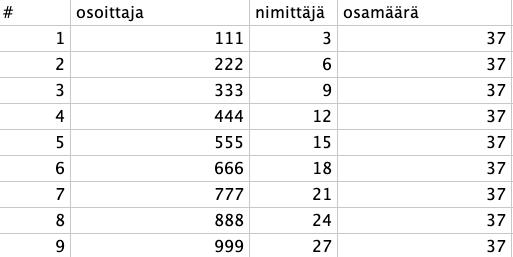
Jos tutkitaan samaa asiaa isommalla lukumäärällä numeroita, vaikkapa viidellä numerolla, niin osamäärä toki muuttuu, mutta se pysyy samana.

Taulukkolaskennassa

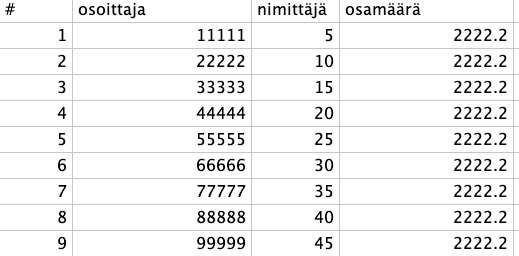
Kokeillaan vielä vaikkapa 15 numerolla

Pohdiskeltavaa

Sovitaan, että a on jokin numeroista 1-9 ja n on osoittajan numeroiden määrä. Näin ollen tutkittava lukumme on 

1. Todista, että kun n on 2, niin osamäärä X pysyy muuttumattomana kaikilla a:n arvoilla.
2. Todista, että jokaista n:n arvoa 1, 2, 3, … vastaa osamäärän arvo, joka on sama kaikilla a:n arvoilla.
3. Määritä osamäärän arvo X(n), kun n = 1, 2, 3, …
   

Lähteet

Luin aiheesta ensimmäisen kerran täältä, “Miraculous world of Numbers” -blogi
https://anil7pute.blogspot.com/2022/12/136-number-pattern-and-its-beauty.html