Innostuin näistä geometrisista kuvioista, kun näin niitä georgialaisen Pridon Davlianidzen postauksissa Facebookin Geomath-ryhmässä. Hän on julkaissut suuren määrän matemaattisia taideteoksia. Ne perustuvat symmetrisiin kuvioihin, jotka tuotetaan säännöllisistä monikulmioista.

Luon pisteet A ja B. Niiden avulla muodostan säännöllisen viisikulmion BACDE, GeoGebrassa valitaan säännöllinen monikulmiotyökalu ja valitaan pisteet B ja A tässä järjestyksessä. Seuraavaksi käytän pisteitä D ja C ja luon niiden avulla säännöllisen viisikulmion DCFGH. Jatkan laatoitusta samalla tapaa 10 viisikulmion saakka. Syntyy kuvio, jota kutsun nimellä säännöllinen monikulmioympyrä. Jos joku keksii tällaisille olioille fiksumman nimen, niin kertokoon minulle.

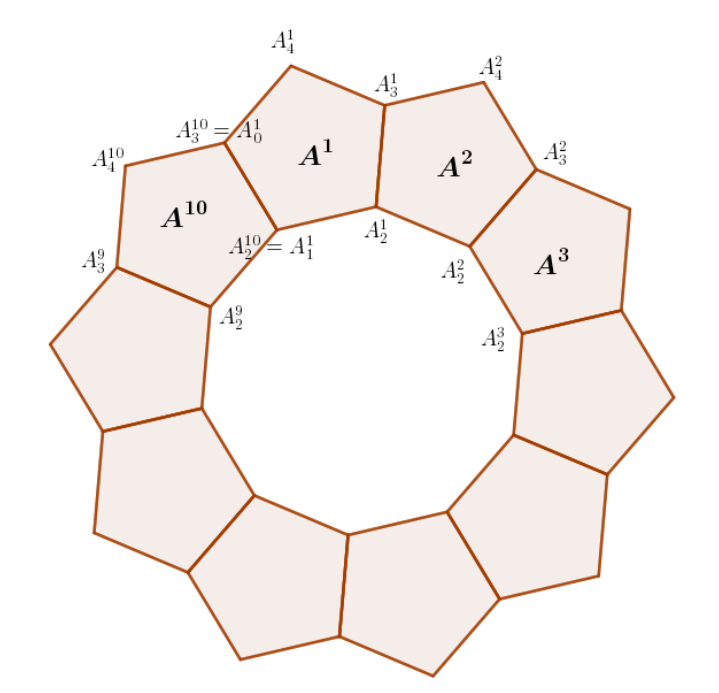
Toki kolmioilla ja neliöilläkin  saa aikaan säännölliset monikulmioympyrät, mutta niiden sisään ei muodostu ”reikää”. Säännöllisillä 6-kulmioilla saadaan kaksi monikulmioympyrää. Säännöllisillä 7-kulmioilla saadaan tällä menetelmällä yksi ympyrä, jossa on 14 säännöllistä 7-kulmiota.

Tehtäviä

Tässä vaiheessa herää joitakin kysymyksiä.

Tehtävä 1. Voiko kaikilla säännöllisillä n-kulmioilla tuottaa säännöllisiä monikulmioympyröitä?

Tehtävä 2. Millä n:n arvoilla saadaan aikaiseksi erilaisia säännöllisiä monikulmioympyröitä, esimerkiksi kun n = 6 voidaan tehdä kaksi erilaista monikulmioympyrää, mutta kun n on 3, 4, 5 tai 7, niin vain yksi.

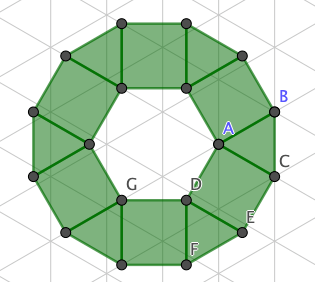
Tehtävä 3. Mitä jos käytetään kahta erilaista säännöllistä monikulmiota, kuten kuvassa. Voiko kaikilla sellaisilla laatoilla, jotka on luotu kahdesta säännöllisestä monitahokkaasta luoda ympyrän?

Lähteet

Geomath-ryhmä Facebookissa
https://www.facebook.com/groups/2224201757729993/?multi_permalinks=2563768697106629&notif_id=1677585820634466&notif_t=group_activity&ref=notif