Pari viikkoa sitten kirjoitin James Tantonin pelistä nimeltä ”a not-exciting game of solitaire”. Artikkelissani esitin todistustehtäviä ja kolme haastavampaa tehtävää. Tutkin tässä joitakin tapoja, miten ratkoa noita haastavampia tehtäviä.
pelin säännöt ja tehtävät
Valitse joukko lukuja. Kutsutaan lukujoukkoa listaksi. Valitse näistä kaksi lukua. Poista ne listalta ja korvaa ne lukujen tulon ja summan summalla. Jatka näin, kunnes listaan jää vain yksi luku.
Haastavampi laskutehtävä 1. Olkoon listassa n kappaletta ykkösiä. Mikä on pelin viimeinen luku. Jos merkitään että f(n) on pelin lopputulos, niin minkä tyyppinen funktio on kyseessä? Lineaarinen, potenssi, eksponentiaalinen, … ?
Haastavampi laskutehtävä 2. Olkoon listassa luvut [1, 2, 3, …, n]. Mikä on pelin viimeinen luku? Minkä tyyppistä on f(n):n kasvu?
Haastavampi laskutehtävä 3. Olkoon listassa luvut [a, b, c, d, …]. Kehitä mahdollisimman yksinkertainen kaava viimeisen luvun laskemiseksi.
Haastavampi laskutehtävä 4. Olkoon listassa alkuperäisen esimerkkien luvut [2, 3, 3, 5, 7]. Lisää listaan yksi luku siten, että pelin viimeinen luku on nolla.
ongelmanratkaisua
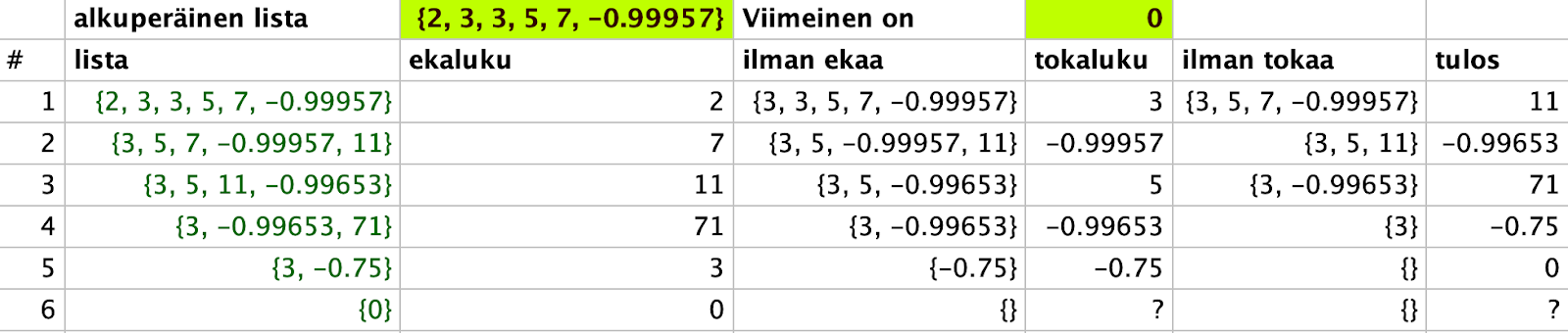
Kun alun perin törmäsin tähän tehtävään, niin aloin pohtia mikä yhteys noilla listan luvuilla ja lopputuloksella oli. Esimerkiksi listalla [2, 3, 3, 5, 7] lopputulos on 2303. Tein GeoGebralla taulukkolaskentasovelluksen, jonka avulla oli helppoa tutkia ongelmaa. Kokeilemalla eri lukulistoja ja tapoja valita poistettavat luvut huomasin, että samalla lukulistalla lopputulos pysyy aina samana, vaikka lukujen arpomisen tekee missä järjestyksessä tahansa.
Laskeskelin viimeistä lukua GeoGebran CAS:ssa, jos listassa on luvut [a, b, c, d].

Itse asiassa jo tuota CAS-tulosta tuijottamalla olisi pitänyt tajuta, millainen riippuvuus listan lukujen ja lopputuloksen välillä on. Algebraa enemmän harrastanut henkilö varmaan näkee kaavan viimeiselle luvulle suoraan noista CAS:in tuottamista lausekkeista.
Lopulta tein Pythonilla koodinpätkän, jonka avulla pystyin pelaamaan monta peliä kerralla. Linkit GeoGebra ja Python -sovelluksiin liittyviin artikkeleihin löytyy lähteet-luvusta. En malta olla käyttämättä Pythonin matplotlib-kirjaston xkcd-funktiota, jonka avulla saan kuvaajistani Randall Munroen XKCD-sarjakuvan tyylisiä. Löysin tuon funktion eilen :o)
ykköslista
Jos listassa on pelkkiä nollia, niin lopputulos on nolla.
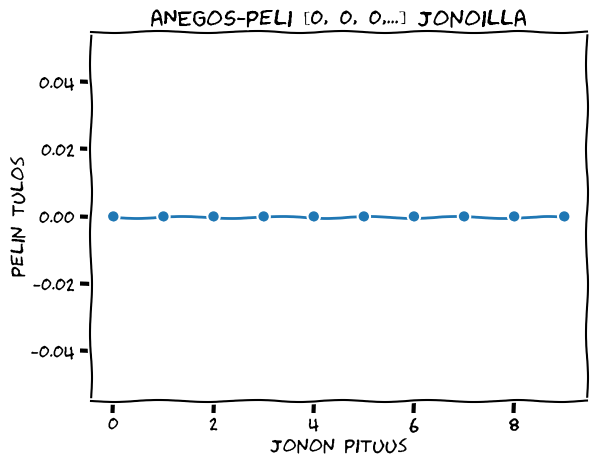
Ykkösillä lopputuloksen arvo alkaa kasvaa aika vikkelästi jonon pituuden kasvaessa. Viidellä ykkösellä [1, 1, 1, 1, 1] lopputulos on 31. Alla olevassa taulukossa kaksi ensimmäistä saraketta ovat satunnaisesti valittuja lukuja ja oikeanpuoleisin luku on niiden tulon ja summan summa.
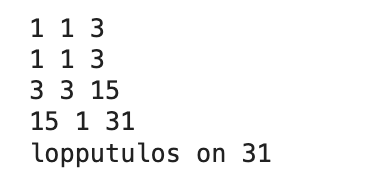
Python-koodini avulla sain oheisen taulukon. Vasen sarake on jonon pituus ja oikea viimeinen luku.

Tuosta voi aika selvästi arvata, että viimeinen luku on kakkosen potenssi + 1.

Haastava tehtävä 1.
Merkitään f(n) = algoritmin lopputulos alkuperäisen jonon [1, 1, … 1] pituuden n funktiona. Tällöin f(n) = 2n - 1.
[1, 2, 3, …, n] -jonot
Tämän tyyppiset jonot kasvavat paljon vikkelämmin.

Alla olevassa kuvaajassa on huomattava, että pystyakselilla yksikkö on 107.

Mitäs lukuja nuo (1, 5, 23, 119, 719, …) ovat? Ykköslistassa luvut olivat yhtä pienempiä kuin 2n. Mitä jos tämän jonon jokaiseen lukuun lisätään ykkönen, niin saadaan (2, 6, 24, 120, 720, …). Nämä näyttävät jo paljon tutummilta. Nehän ovat kertomia. 2! = 2, 3! = 3*2 = 6, 4! = 4*3*2 = 24, ….
Haastava tehtävä 2.
Jos merkitään g(n) = pelin lopputulos, kun alkuperäinen lista on [1, 2, 3, …, n], niin g(n) = (n+1)! - 1
yleinen kaava
Edelliset tulokset helpottavat kaavan löytämisessä, kun alkuperäinen lista on [a, b, c, …]. Kun artikkelin alun GeoGebra CAS-laskun viimeisen rivin tulokseen lisätään 1 ja jaetaan se tekijöihin niin saadaan kaunis kaava.
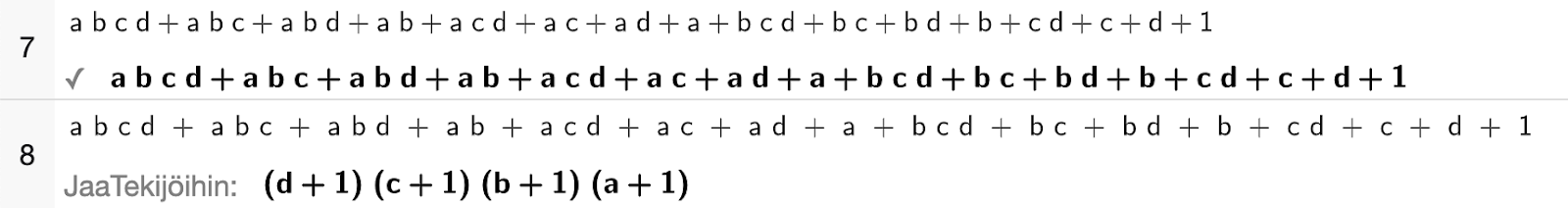
Haastava tehtävä 3.
Jos merkitään T(a, b, c, ...) = pelin lopputulos, kun alkuperäinen lista on [a, b, c, …] , niin T(a, b, c, ...) = (a+1)(b+1)(c+1) … - 1.
Lasketaan tarkistuksen vuoksi aiemmin esitetyillä listoilla.
[2, 3, 3, 5, 7]
3*4*4*6*8 – 1 = 2303
n kappaletta nollia [0, 0, …]
1*1*…*1 - 1 = 0
n kappaletta ykkösiä [1, 1, 1, …]
2*2*… – 1 = 2n – 1
[1, 2, 3, 4, … n]
2*3*4*… (n+1) – 1 = (n+1)! – 1
Jätän tämänkin tuloksen yleisen todistuksen harjoitustehtäväksi minua matemaattisesti fiksuimmille.
neljäs haastavampi tehtävä
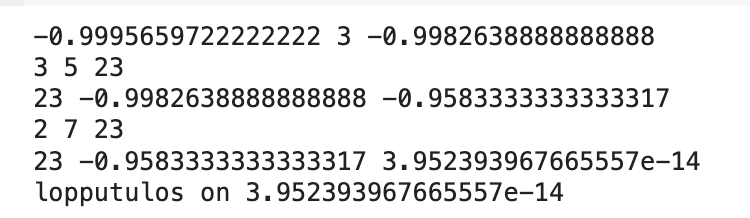
Nyt kun meillä on yleinen kaava, niin tuon [2, 3, 3, 5, 7, x] ongelman ratkaisu on helppo vaikkapa CAS:illa.
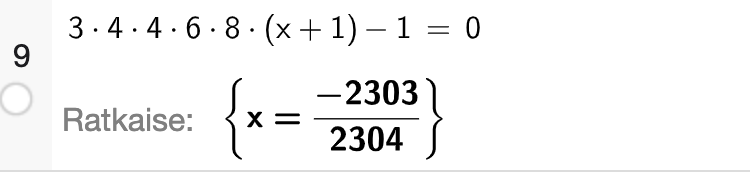
Alla Pythonilla ja GeoGebralla laskettu tarkistus, kun alkuperäinen lista on [2, 3, 3, 5, 7, -2303/2304].
lähteet
A not-exciting game of solitaire, peli yhteen- ja kertolaskun harjoitteluun
https://mikkorahikka.blog/2024/01/28/a-not-exciting-game-of-solitaire-peli-yhteen-ja-kertolaskun-harjoitteluun/
Tantonin aNEGoS-peli GeoGebralla
https://mikkorahikka.blog/2024/02/04/tantonin-anegos-peli-geogebralla/
Tantonin aNEGoS-peli Pythonilla
https://mikkorahikka.blog/2024/02/11/tantonin-anegos-peli-pythonilla/

Jätä kommentti