[edit. 20.10.24 korjasin vioittuneen kaavan.]
Tutkitaan kolmiolukujen käänteisluvuista muodostetun sarjan suppenemista. Tähän tarinaan sain idean David Meyerin mathsdoton.xyz-viestistä.
Kolmioluvuiksi kutsutaan lukuja 1, 3, 6, 10, 15, 21, …. Jos käytössä on kolmioluvun verran biljardipalloja, niin ne saa kasattua kolmioiksi kuvan tapaan.
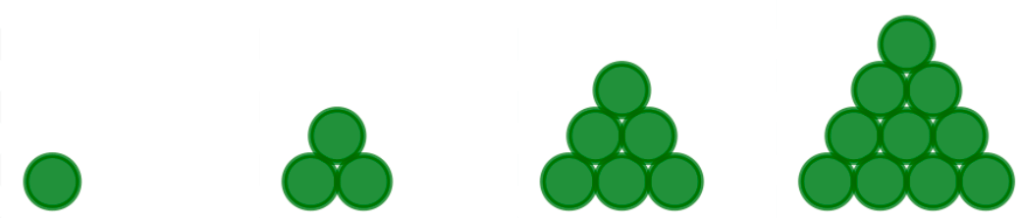
Kolmioluvut saa laskettua n:n arvoilla 1, 2, 3, … kaavalla

Varmaan aika moni tämän blogin lukijoista tietää, että harmoninen sarja

kasvaa rajatta. Miten käy sarjalle, jossa lasketaan yhteen kolmiolukujen käänteisluvut.
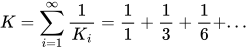
Kun summien arvoja laskee ja muodostaa niistä pisteistöt koordinaatistoon, niin saa jonkinlaisen kuvan sarjojen käyttäytymisestä.
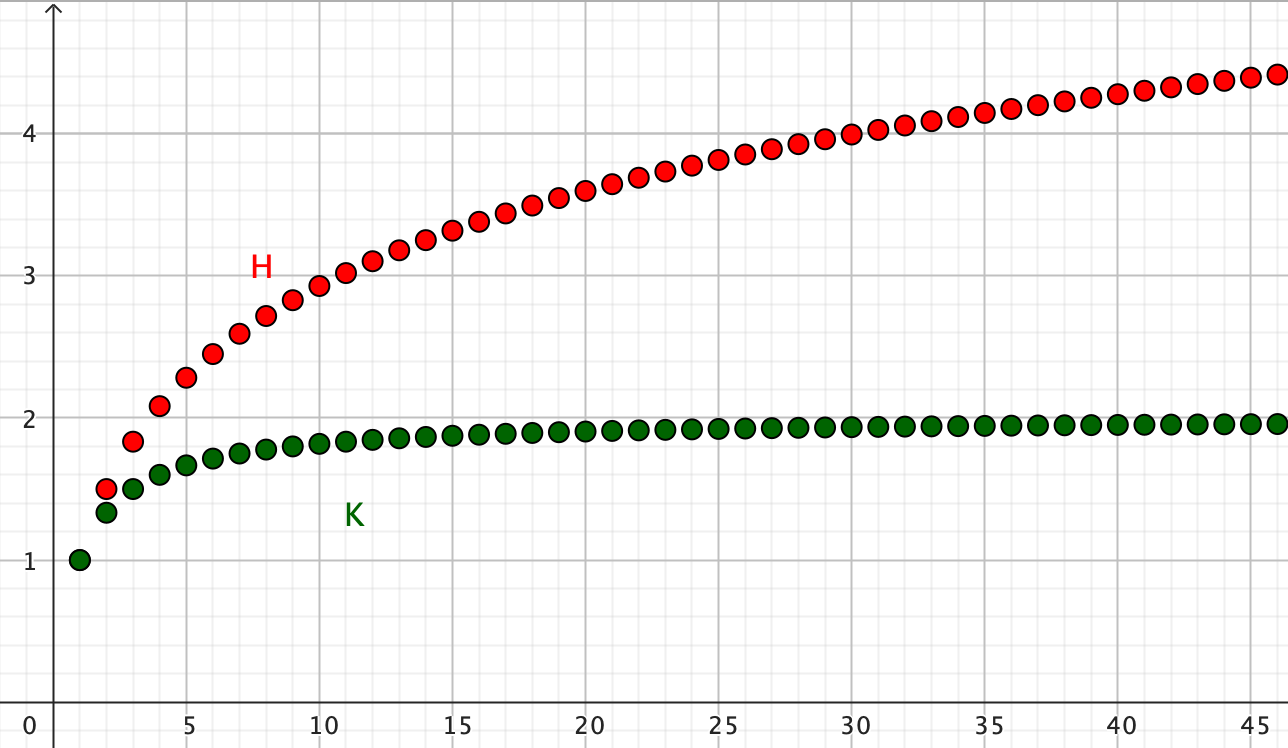
Harmoninen sarja H kasvaa rajatta, tosin aika hitaasti. Tutkittava K-sarjan arvot näyttävät pysyvän kakkosen alapuolella. Vaikuttaa siltä, että sarja suppenee. Nyt vaan pitäisi todistaa se. Jätän todistuksen lukijalle ja avuksi liitän toisen helpon ongelman, jota voi käyttää K-sarjan suppenemisen todistuksen apuna. Ja toki suppenemisen voi todistaa käyttämättä apuna ilman tuota apulausetta. Parhaat laskijat pystyvät tuottamaan todistukset ilman CAS-laskimen apuja :o)
Ongelma 1. Todista. Kun n ≠ 0 tai n≠ -1 , niin peräkkäisten lukujen käänteislukujen tulo on yhtä suuri kuin niiden käänteislukujen erotus
Ongelma 2. Todista, että kolmiolukujen Ki käänteisluvuista muodostettu sarja suppenee
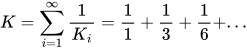
Palannen lähiaikoina kolmiolukujen ominaisuuksiin.
lähteet
Harmoninen sarja Wikipediassa
https://fi.wikipedia.org/wiki/Harmoninen_sarja
Kolmioluvut Wikipediassa
https://fi.wikipedia.org/wiki/Kolmioluku
David Meyer Mathsdoton.xyz viesti
https://mathstodon.xyz/@dmm/112264366740352480

Jätä kommentti