geometria
-
2025 Pythagoraan kolmikot ja nelikot

[edit. 4.1.25. korjasin vuosiluvun viimeisessä virkkeessä.] Luku 2025 on mielenkiintoinen, kuten kaikki luvut. Päätinpä tutkia yhtälöiden x2 + y2 = 20252 ja x2 + y2 + x2= 20252 kokonaislukuratkaisuja. Apuna käytin Pythonia ja GeoGebraa. Tein muutaman Python koodinpätkän, joiden avulla tuotin taulukot, ratkaisut ja kuvaajat. Jos haluat itse katsella interaktiivisia kuvaajia, niin lähetä minulle sähköpostia… Continue reading
-
Suurin kolmio säännölliseen monikulmioon
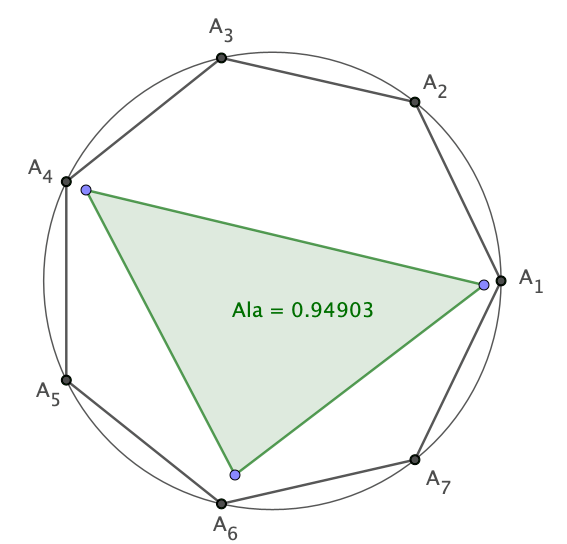
Tässä ongelmassa tutkitaan säännöllisiä monikulmioita, joiden kärjet ovat yksikköympyrällä. Kuinka suuri on alaltaan suurin kolmio, joka mahtuu monikulmion sisälle? Käytän esimerkkinä yksikköympyrään piirrettyä säännöllistä heptagonia eli seitsenkulmiota A1, A2, … , A7. Kun tätä ongelmaa alkaa pohdiskella, niin huomaa aika aikaisessa vaiheessa, että alaltaan suurimman kolmion kärkien täytyy olla monikulmion sivuilla tai kärkipisteissä. Tein GeoGebralla… Continue reading
-
Hilapisteitä ympyröiden sisälle
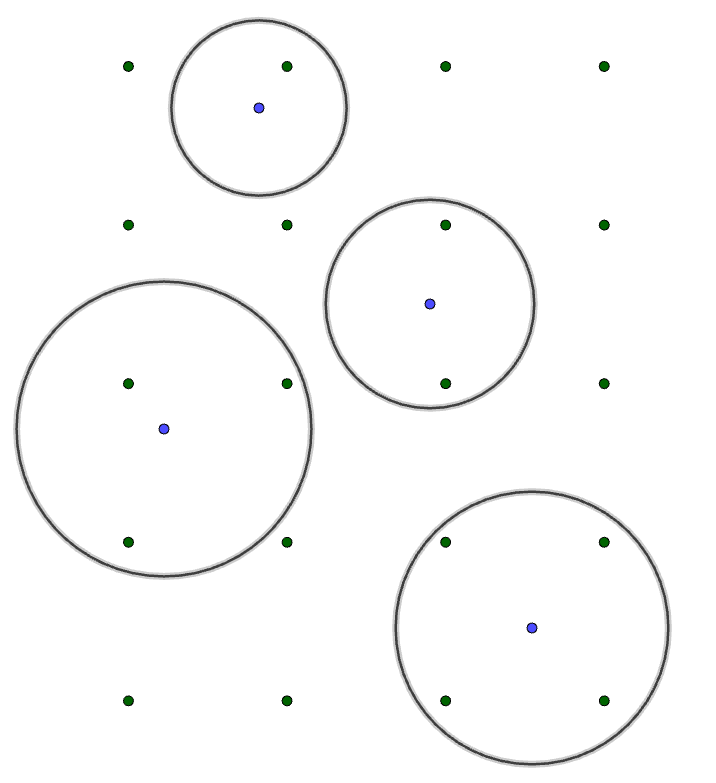
Kuvassa on piirretty ympyröitä siten, että niiden sisälle jää 1, 2, 3, ja 4 hilapistettä. Onko tämä aina mahdollista? Hilapisteillä tarkoitetaan sellaisia tason pisteitä, joilla molemmat koordinaatit ovat kokonaislukuja. Ongelma 1. Olkoon N jokin aidosti positiivinen luonnollinen luku (1, 2, 3, …). Onko mahdollista piirtää tasoon sellainen ympyrä, että ympyrän sisälle jää tasan N kappaletta… Continue reading
