kolmio
-
Suurin kolmio säännölliseen monikulmioon
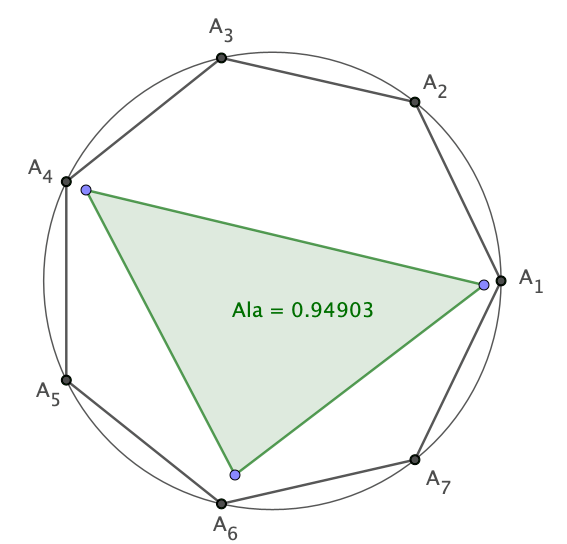
Tässä ongelmassa tutkitaan säännöllisiä monikulmioita, joiden kärjet ovat yksikköympyrällä. Kuinka suuri on alaltaan suurin kolmio, joka mahtuu monikulmion sisälle? Käytän esimerkkinä yksikköympyrään piirrettyä säännöllistä heptagonia eli seitsenkulmiota A1, A2, … , A7. Kun tätä ongelmaa alkaa pohdiskella, niin huomaa aika aikaisessa vaiheessa, että alaltaan suurimman kolmion kärkien täytyy olla monikulmion sivuilla tai kärkipisteissä. Tein GeoGebralla… Continue reading
-
Kolmion sivujen keskipiste -iterointi
Pari viikkoa sitten kirjoitin aika haastavasta ympyrämonikulmioiteroinnista. Siinä iteroinnin raja arvo päätyy Kepler–Bouwkamp -vakioon. Tutkitaan hieman yksinkertaisempaa ongelmaa liittyen kolmion sivujen keskipisteistä muodostettujen kolmioiden iterointiin. Luodaan kolmio ABC. Tämän jälkeen luodaan uusi kolmio käyttämällä janojen AB, BC ja CA keskipisteitä. Jatketaan samalla tavalla syntyvien kolmioiden kärkipisteillä. Mihin pisteeseen päädytään? Tai paremminkin. Mitä pistettä kohden kolmioiden… Continue reading
-
Pythagoras toisinpäin
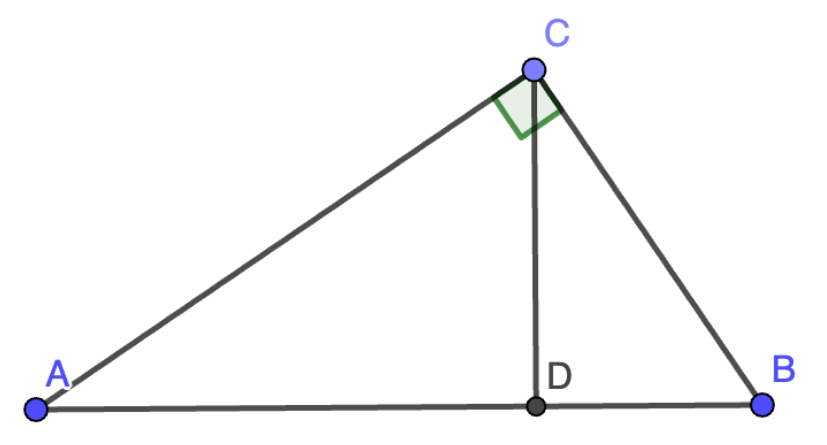
Tämän todistaminen sopii nuorille, kun he tutustuvat kolmioihin ja Pythagoraan lauseeseen. Tälle löytyy varmaan aika monta erilaista todistusta. Todista. Kuvan suorakulmaisessa kolmiossa ABC pätee yhtälö lähde Inside Out Futility Closetissahttps://www.futilitycloset.com/2024/07/19/inside-out-4/ Continue reading
