pythagoras
-
2025 Pythagoraan kolmikot ja nelikot

[edit. 4.1.25. korjasin vuosiluvun viimeisessä virkkeessä.] Luku 2025 on mielenkiintoinen, kuten kaikki luvut. Päätinpä tutkia yhtälöiden x2 + y2 = 20252 ja x2 + y2 + x2= 20252 kokonaislukuratkaisuja. Apuna käytin Pythonia ja GeoGebraa. Tein muutaman Python koodinpätkän, joiden avulla tuotin taulukot, ratkaisut ja kuvaajat. Jos haluat itse katsella interaktiivisia kuvaajia, niin lähetä minulle sähköpostia… Continue reading
-
Pythagoras toisinpäin
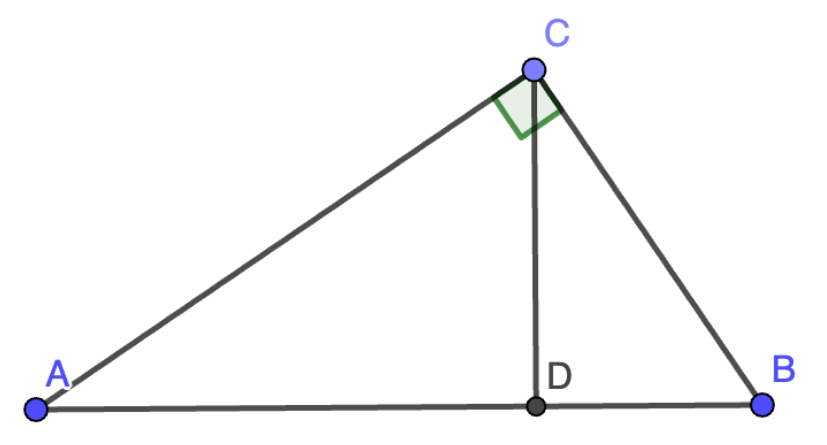
Tämän todistaminen sopii nuorille, kun he tutustuvat kolmioihin ja Pythagoraan lauseeseen. Tälle löytyy varmaan aika monta erilaista todistusta. Todista. Kuvan suorakulmaisessa kolmiossa ABC pätee yhtälö lähde Inside Out Futility Closetissahttps://www.futilitycloset.com/2024/07/19/inside-out-4/ Continue reading
-
Käänteinen Pythagoras – ongelma
[edit. 18.3.24. korjasin kolmikkojen määrittelyn järkevämmäksi.] Kun jossain näen ongelman, joka jotenkin liittyy Pythagoraan lauseeseen, niin päässäni alkaa pörrätä mehiläisiä. James Tantonin X-tweetissä oli simppeli kysymys. Onko ”käänteisellä” Pythagoraan lauseella 1/a2 + 1/b2 = 1/c2 ratkaisuja? Onhan sillä. Tantonin alkuperäinen tweetti. käänteiset Pythagoraan kolmikot Käänteiset Pythagoraan kolmikot a, b, c ovat luonnollisia lukuja (1, 2,… Continue reading
