python
-
Abitti 2:n Abicoden Pythonin matemaattiset moduulit – math, random, statistics, decimal, fraction

Python sisältää on runsaasti erilaisia moduuleja. Tässä tutkailen millaisia matemaattisia kirjastoja on Abitti 2:n Abicodessa. Esitän esimerkkien avulla joitakin math, random, statistics, decimal ja fractions moduulien funktioita. Valitsen esimerkkeihin sellaisia funktioita, joista voisi teoriassa olla lukiolaisille apua pitkän tai lyhyen matikan opinnoissa ja ylioppilaskirjoituksissa. Tarinan lopun lähteissä on linkki tiedostoon, jossa on Googlen Colabissa samat… Continue reading
-
xkcd sammakon pakonopeus/pakosäde

Tällä viikolla ilmestyneessä xkcd:ssä käsitellään taivaankappaleen sädettä, jotta sammakko hypätessään ei putoaisi takaisin kappaleen pinnalle. Tutkitaan asiaa hieman tarkemmin. Tässä Randall Munroe olettaa, että kun sammakko hyppää ylöspäin, sen nopeus on 4,5 m/s. Tämä nopeus on aika lähellä ihmisen maksiminopeutta kun ponnistetaan ylöspäin. Guinnessin ennätysten kirjan mukaan Darius Clark hyppäsi vuonna 2022 1,27 m:n korkeuteen.… Continue reading
-
Lukiot järjestykseen
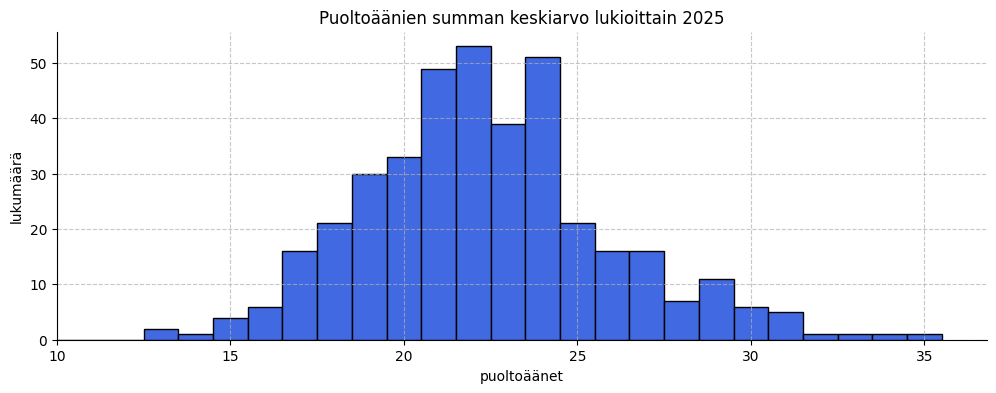
[edit. 12.12.25 Lisäsin kommentin lukioiden oppilasmääristä tietoa lukioista -lukuun. 18.1.26 Korjasin pari kirjoitusvihrettä.] Olen viime aikoina tutkiskellut Ylioppilaslautakunnan julkaisemia tilastoja ylioppilaista. Teinpä sitten pienen koodin, jonka avulla voi laittaa lukioita ”paremmuusjärjestykseen”. Laitan sanan ”paras” lainausmerkkeihin, sillä tarkoitan tässä tarinassa järjestystä, joka on mitattu puoltoäänien keskiarvon mukaan. Minun mielestäni kouluja oikeasti ei voi laittaa paremmuusjärjestykseen, kaikki… Continue reading
