Yritin keksiä todistusta Marionin lauseeseen (Marion’s Theorem). Kun piirsin kuviota GeoGebralla, tein virheen tuottaessani kuusikulmiota kolmion sisään. Löysin uusia totuuksia liittyen kolmion sisään piirrettyihin kuusikulmioihin.  

Kolmiossa ABC pisteet D ja E jakavat janan AB suhteessa 1:1:1 eli janojen AD ja BE pituudet ovat ⅓ janan AB pituudesta. Vastaavasti F ja G jakavat janan BC suhteessa 1:1:1 ja janat H ja I jakavat janan CA suhteessa 1:1:1. Muodostetaan janat DF, FH, HD, EG, GI ja IE. Nämä janat leikkaavat toisensa pisteissä J,K,L,M,N ja O. 

helpot ongelmat

Näistä kannattanee aloittaa kolmannesta, se taitaa olla helpoin. Laitan nämä ongelmat siihen järjestykseen, kun itse ne keksin GeoGebra kokeilujeni avulla.

 Ongelma 1. Kolmion ABC ja kuusikulmion JKLMNO alojen suhde on 9/2. Todista.

Ongelma 2. Kuvioon muodostuu kuusisakarainen tähtikuvio DJEKFLGMHNIO. Todista, että kolmion ABC ja tähtikuvion alojen suhde on 9/4.

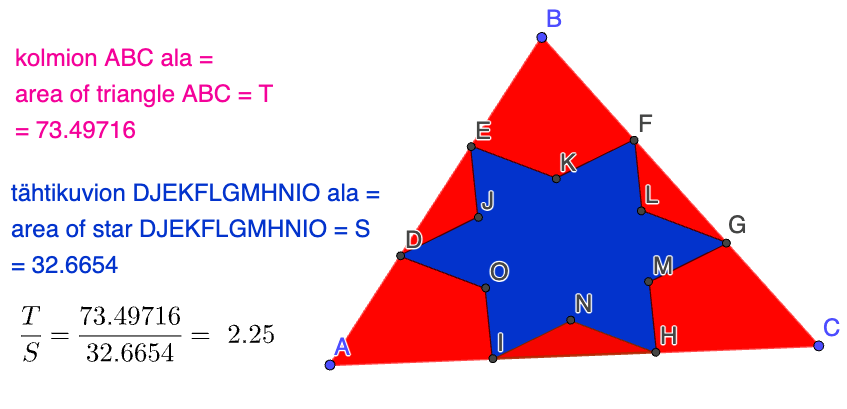
Ongelma 3. Kolmion ABC ja kuusikulmion DEFGHI alojen suhde on 3/2. Todista.

Kun olin tarpeeksi puuhastellut tämän kuvion avulla, päätin kokeilla mitä tapahtuu, kun muutan jakosuhdetta. Olkoon u luku välillä ]0, 1/2[. Pisteet D ja E jakavat janan AB suhteessa u : 1 – 2 u : u. Nyt janat AD/AB  = BE/AB = u. Vastaavasti pisteet F ja G jakavat janan BC sekä pisteet H ja I jakavat janan CA suhteessa u : 1 – 2 u : u.

Mikon kuusikulmio kolmiossa-lauseet

I Kolmion ABC ja kuusikulmion JKLMNO alojen suhde on vakio.

II Kolmion ABC ja tähtikuvion DJEKFLGMHNIO alojen suhde on vakio.

III Kolmion ABC ja kuusikulmion DEFGHI alojen suhde on vakio.

eikä siinä vielä kaikki

Kokeilin vielä suoria, jotka kulkevat sisimmmän kuusikulmion sivujen jatkeina ja sitä kautta sain aikaan uuden kolmion. Olkoon piste U suorien DF ja IG leikkauspiste,  piste R suorien EG ja DH leikkauspiste ja piste Q suorien IE ja HF leikkauspiste. 

Mikon kuusikulmiolause IV.  Kolmioiden ABC ja UQR alojen suhde on vakio. 

Osaan lauseitani minulla on suhteellisen suhteellisen rumat ratkaisut, jossa käytän koordinaatistoa ja hurjaa määrää yhtälöitä, joiden avulla saadaan suorien leikkauspisteet ja sitä kautta alat. Myös ChatGPT ratkaisee ongelmat samalla tavalla. En ole löytänyt fiksua geometrista todistusta lauseilleni.  Toki käyttämällä kolmion alan kaavaa kanta*korkeus/2 ja yhdensuuntaisia useamman kerran tuottanee ainakin osaan lauseista mielekkään todistuksen, samaan tyyliin kuin Marionin lauseen todistuksessa WolframMath Worldissä.

Omasta mielestäni en ole aiemmin törmännyt näihin lauseisiin. Pienen haeskelun ja AI-keskustelujen jälkeen löysin Routhin teoreeman, joka on vähän samantyyppinen. Kerro minulle, jos kyseiset geometrian lauseet on julkaistu jossain aiemmin.

Alla vielä kuvat, joiden tarkoitus on havainnollistaa kaikkia neljää lausetta. Kuvissa on samalla u:n arvolla kaksi eri kolmiota ABC ja lauseissa esitetyt suhteet. Näissä on alojen arvot ovat pienillä kirjaimilla.

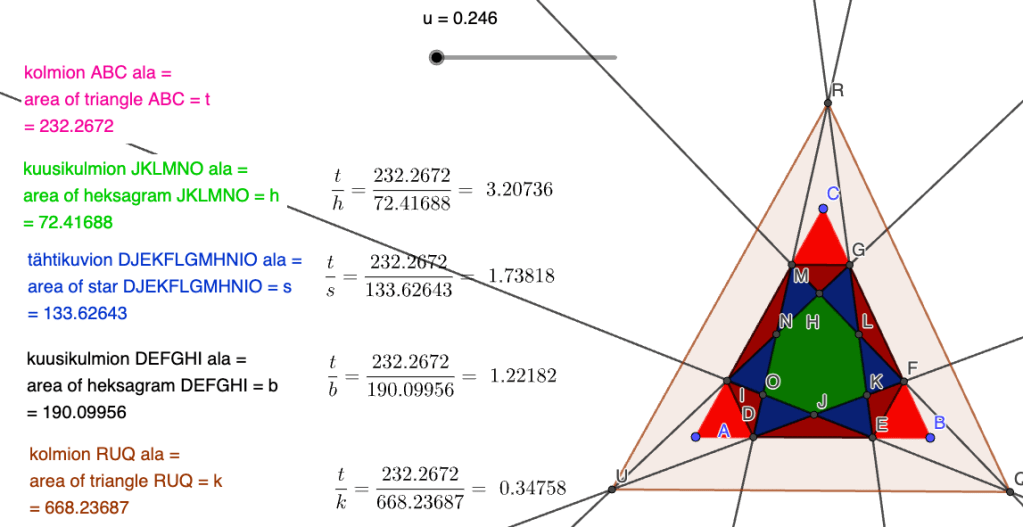
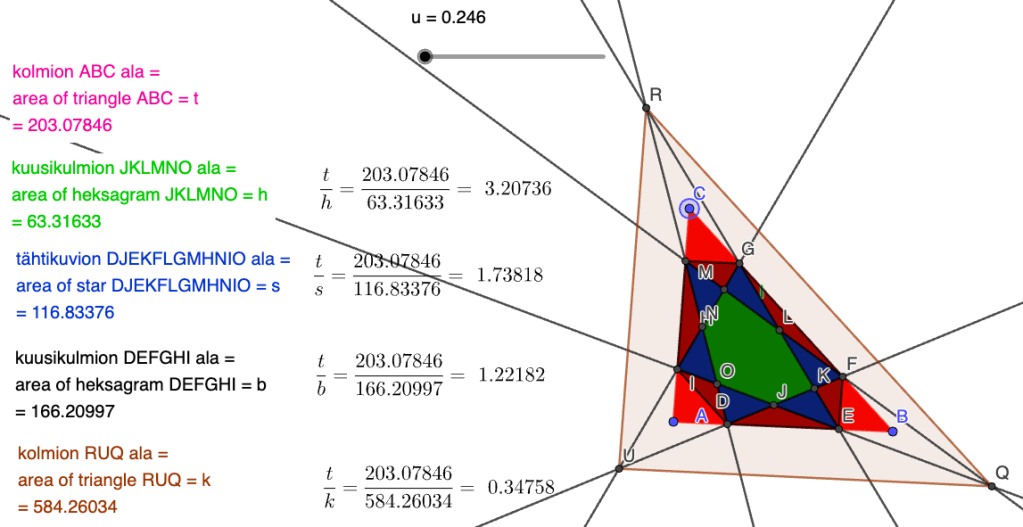
lähde

Marion’s Theorem Wolfram Math Worldissä
https://mathworld.wolfram.com/MarionsTheorem.html

Routh’s theorem Wikipediassa
https://en.wikipedia.org/wiki/Routh%27s_theorem

Mikko’s theorems on heksagram in triangle
https://www.geogebra.org/m/habevzue