geometria
-
Omituinen ”nelikulmio” -ongelma

Eiväthän nämä oikeasti ole nelikulmioita tai suorakaiteita. Paitsi jos sovitaan, että ympyrän kaari voi olla neliön sivu. Kuvan ”suorakaiteissa” on kaksi janaa ja kaksi ympyrän kaarta. Ympyränkaaret ovat kohtisuorassa sivuja vastaan. Tutkitaan näiden kahden ”suorakaiteen” pinta-aloihin ja piireihin liittyviä ongelmia. Harmaa ”suorakaide” on piirretty siten, että aluksi on luotu kaksi ympyrää, joiden keskipiste on piste… Continue reading
-
Öismäe-ongelma
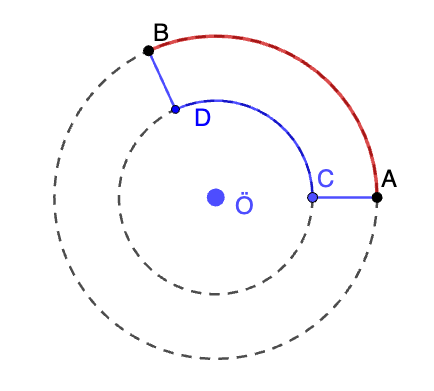
Kuulin alun perin tämän tehtävän virolaiselta ystävältäni Hannes Jukkilta. Hänen ongelmansa liittyi Tallinnassa sijaitsevaan Väike-Öismäe Tiik nimiseen lampeen ja sitä kiertäviin ympyrän muotoisiin katuihin. Pohditaan millainen reitti on lyhin kahden saman kadun varrella olevan paikan välillä. Tehtävä on julkaistu vuonna 1969 Levinien kirjassa Matemaatika ülesannete kogu keskkoolile. Minusta tuo reitti ACBD pitää olla ACDB. Muokkaan ongelman… Continue reading
-
Ison kirjan alaongelma

Tutkitaan vanhaa pinta-aloihin liittyvää ongelmaa. Se löytyy Isosta Kirjasta. Olen julkaissut vastaavan tarinan Hyllin vanhoilla veppisivuilla joskus 2011 tai aiemmin. Kahden ensimmäisen ongelman todistaminen on suhteellisen helppoa. Jäljennän alle GeoGebralla tuotetun kuvan, joka löytyy englanninkielisestä Newtonin Principiasta. Book I. Section II. To find centripetal forces. Proposition I, Theorem I. Ongelma 1. Olkoot A, B ja… Continue reading
