monikulmio
-
Suurin kolmio säännölliseen monikulmioon
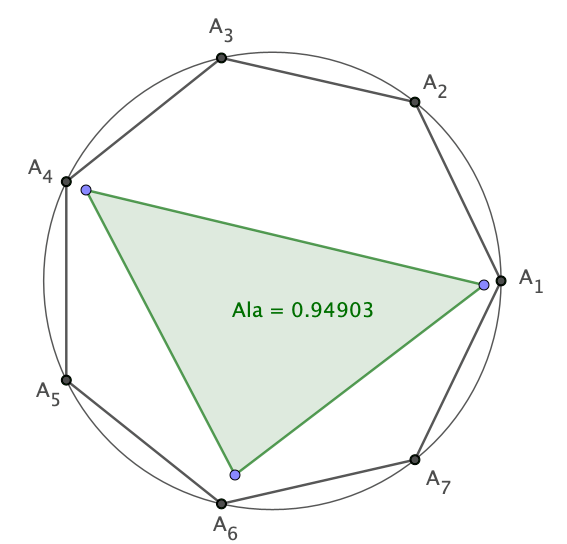
Tässä ongelmassa tutkitaan säännöllisiä monikulmioita, joiden kärjet ovat yksikköympyrällä. Kuinka suuri on alaltaan suurin kolmio, joka mahtuu monikulmion sisälle? Käytän esimerkkinä yksikköympyrään piirrettyä säännöllistä heptagonia eli seitsenkulmiota A1, A2, … , A7. Kun tätä ongelmaa alkaa pohdiskella, niin huomaa aika aikaisessa vaiheessa, että alaltaan suurimman kolmion kärkien täytyy olla monikulmion sivuilla tai kärkipisteissä. Tein GeoGebralla… Continue reading
-
Ympyrämonikulmiot
Piirrä ympyrä, jonka säde on 1. Piirrä ympyrän sisään tasasivuinen kolmio. Piirrä kolmion sisään ympyrä. Jatka samalla tavalla, mutta seuraavalla kerralla piirrä neliö, seuraavalla säännöllinen 5 kulmio. Jatka n kertaa. Kun n kasvaa, niin ympyröiden säteet pienenevät, mutta vaikuttaa siltä, että ympyröiden säteiden muodostama jono suppenee kohden lukua x. Säteiden jonon alkua viiden desimaalin tarkkuudella… Continue reading
-
Monikulmioympyrät
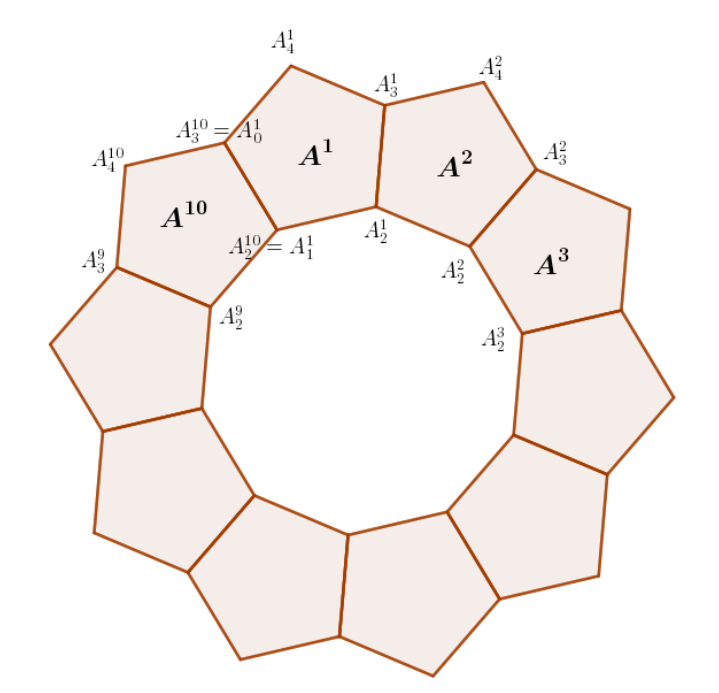
Innostuin näistä geometrisista kuvioista, kun näin niitä georgialaisen Pridon Davlianidzen postauksissa Facebookin Geomath-ryhmässä. Hän on julkaissut suuren määrän matemaattisia taideteoksia. Ne perustuvat symmetrisiin kuvioihin, jotka tuotetaan säännöllisistä monikulmioista. Luon pisteet A ja B. Niiden avulla muodostan säännöllisen viisikulmion BACDE, GeoGebrassa valitaan säännöllinen monikulmiotyökalu ja valitaan pisteet B ja A tässä järjestyksessä. Seuraavaksi käytän pisteitä D… Continue reading
