ongelma
-
Regiomontanuksen 3D tauluongelma
Edellisessä artikkelissani pohdiskelin ongelmaa, joka oli versio alkuperäisestä Regiomontanuksen tauluongelmasta vuoden 1471. Alkuperäinen ongelma on tasogeometrian ongelma. Tosimaailmassa taulut asustavat kolmiulotteisessa maailmassa. Miten ongelma muuttuu? Continue reading
-
Jalkapallomaaliongelma
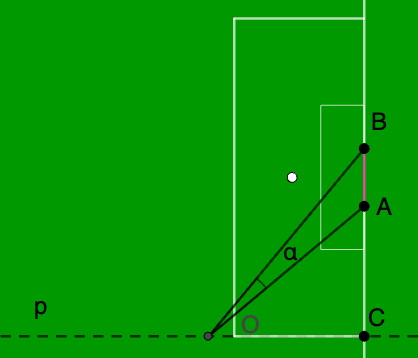
Tämä klassikkotehtävä on nimetty kauan sitten eläneen henkilön nimen mukaan. Alla on hänen kuvansa. Tämän ongelman voi ratkaista kynällä ja paperilla geometrisesti tai sitten kirjainlaskennolla vaikkapa CASia apuna käyttäen. Continue reading
-
Geometrinen snookerlyöntiongelma
[edit. 17.2.25 korjasin vialliset kuvaajatiedostot.] Luin kirjan nimeltä ”Why do buses Come in Threes?”. Kirjassa on paljon tarinoita tosielämän matemaattisista ilmiöistä. Siinä oli selitetty muun muassa miksi biljardin/snookerin pitkissä lyönneissä vaikeinta on saada pallo pussitettua, kun kohdepallo on noin puolessa välissä lyöntipalloa ja pussia. En ollut tyytyväinen kirjan esittämään kaavaan. Piti laskea itse. Tässä tutkitaan… Continue reading
