yksikkömurtoluku
-
Luku 2026
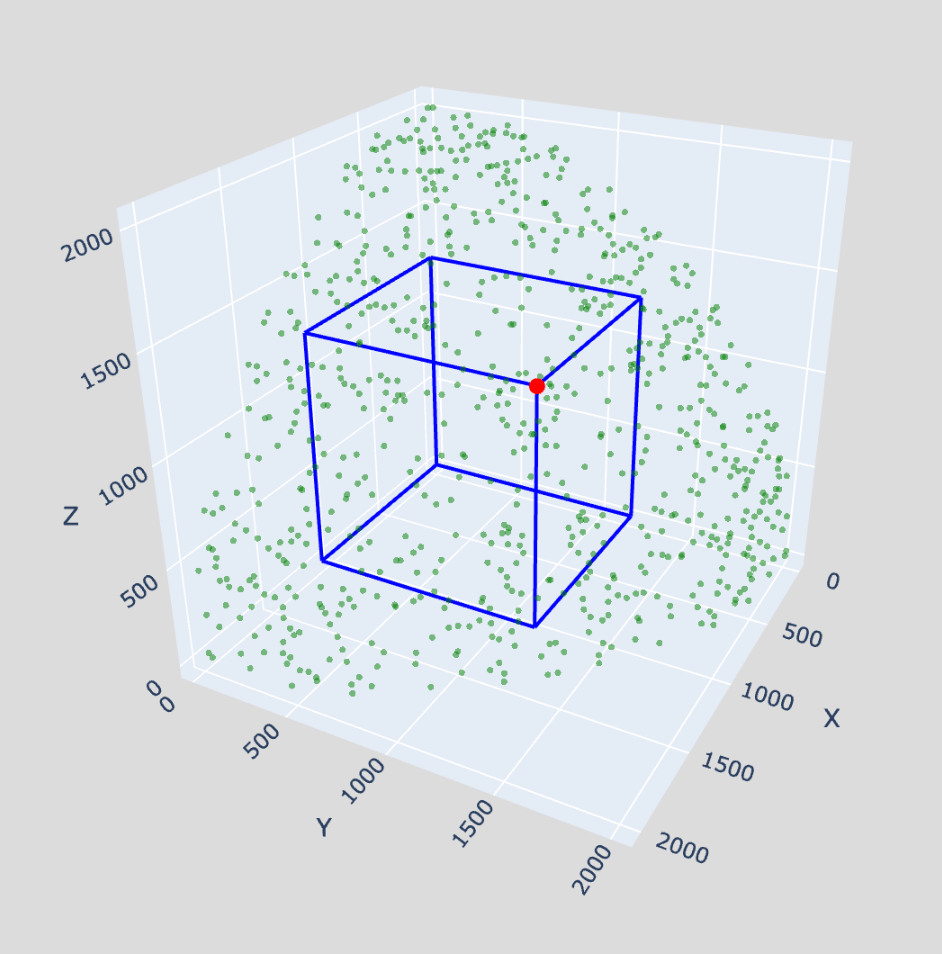
Vuosi vaihtui ja saimme uuden vuosiluvun. Tutkitaan joitakin lukuun 2026 liittyviä kummallisuuksia tai itsestäänselvyyksiä. Keskityn tässä lukuun 1/2026 jaksollisena desimaalilukuna ja yhtälöiden x2 + y2 = 20262 ja x2 + y2 + z2 = 20262 kokonaislukuratkaisuihin. Luvun 2026 alkutekijät ovat 2 ja 1013. Niinpä 10132 + 10132 + 10132 + 10132 = 20262. Geometrinen todistus… Continue reading
-
1/2023 desimaalilukuna
Uuden vuoden kunniaksi. Haaveeni tälle vuodelle on, että oikeasti opin ymmärtämään, miten päätellä tuo jakson pituus käyttämällä vain tietoa, että 2013 = 7*17*17. Ehkä tarvitsen tietoa myös muutamien muiden yksikkömurtolukujen jaksojen pituuksista. Luvun 1/2023 desimaaliesityksen jakson pituus on 816. Ja jakso on 000494315373208106772120612951062778052397429560059317844784972812654473554127533366287691547207118141374196737518536826495304003954522985664854176964903608502224419179436480474542758279782501235788433020266930301532377656945130993573900148294611962432031636183885318833415719228868017795353435491843796342066238260009886307464162135442412259021255561047948591201186356895699456253089471082550667325753830944142362827483934750370736529906080079090459713297083539298072170044488383588729609490855165595650024715768660405338606030647553138902619871478002965892239248640632723677706376668314384577360355907068709836875926841324765200197726149283242708848245180425111220958971824023727137913989125061789421651013346515076618882847256549678695007414730598121601581809194265941670785961443400889767671774592189817103311913 Laitetaan tuohon alle vielä varmuuden vuoksi kaksi jaksoa 0.000494315373208106772120612951062778052397429560059317844784972812654473554127533366287691547207118141374196737518536826495304003954522985664854176964903608502224419179436480474542758279782501235788433020266930301532377656945130993573900148294611962432031636183885318833415719228868017795353435491843796342066238260009886307464162135442412259021255561047948591201186356895699456253089471082550667325753830944142362827483934750370736529906080079090459713297083539298072170044488383588729609490855165595650024715768660405338606030647553138902619871478002965892239248640632723677706376668314384577360355907068709836875926841324765200197726149283242708848245180425111220958971824023727137913989125061789421651013346515076618882847256549678695007414730598121601581809194265941670785961443400889767671774592189817103311913000494315373208106772120612951062778052397429560059317844784972812654473554127533366287691547207118141374196737518536826495304003954522985664854176964903608502224419179436480474542758279782501235788433020266930301532377656945130993573900148294611962432031636183885318833415719228868017795353435491843796342066238260009886307464162135442412259021255561047948591201186356895699456253089471082550667325753830944142362827483934750370736529906080079090459713297083539298072170044488383588729609490855165595650024715768660405338606030647553138902619871478002965892239248640632723677706376668314384577360355907068709836875926841324765200197726149283242708848245180425111220958971824023727137913989125061789421651013346515076618882847256549678695007414730598121601581809194265941670785961443400889767671774592189817103311913000 Continue reading
-
ChatGPT osaa koodata aika hyvin, mutta matikassa on opiskelemista
Viime aikoina on Internet-keskusteluissa (ainakin minun kuplassani) on kohistu jonkin verran tekoälystä ja erityisesti OpenAI:n ChatGPT:stä. Tutkailen tässä miten se osaa ohjelmoida pikku koodinpätkiä. Tuotettu koodi näyttää hyvältä, mutta jotta tulos olisi oikea, niin tekoälyä pitää opettaa. Olen tutkiskellut yksikkömurtolukuja 1/1, ½, ⅓, … ja niiden desimaalikehitelmien jakson pituuksia. Ensimmäiset versiot koodistani löytyvät syyskuun artikkelistani… Continue reading
