kultainen leikkaus
-
Piispan hattu -ongelma
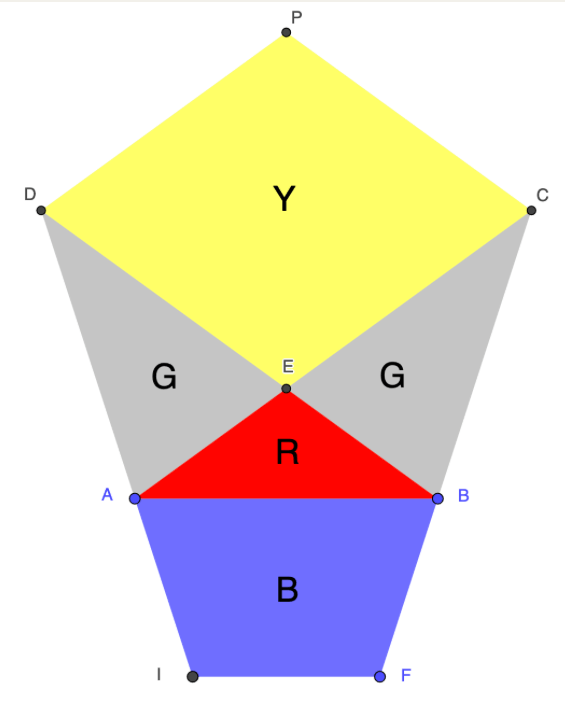
Kaksi säännöllistä viisikulmiota muodostavat piispan hatun/hiipan muotoisen kuvion. Tutkitaan kuvioon muodostuneiden monikulmioiden pinta-alojen suhteita. Alla olevassa kuvassa ABCPD ja IFBEA ovat säännöllisiä viisikulmioita. Piste E on janojen AC ja BD leikkauspiste. Nimetään pinta-alat kuten kuvassa: Y = keltaisen nelikulmion ECPD ala, G = harmaan kolmion AED ala = kolmion BCE ala, R = punaisen kolmion Continue reading
-
Fibonaccitulosumman lauseke
[edit. 19.11.22 lisäsin jälkihuomautuksen loppuun ja linkin Simo Kivelän blogiin] Pari viikkoa sitten kirjoitin minulle uudesta Fibonaccilukuihin liittyvästä totuudesta. Yritin ratkoa sitä eri tavoilla, mutta lausekkeet olivat niin sekavan näköisiä silmissäni, että en uskaltanut alkaa pohtia ratkaisua sen tarkemmin. Aiheeseen liittyvä artikkeli on täällä https://mikkorahikka.blog/2022/10/27/uusi-fibonaccilukujono-ongelma/ Muistin visrkistykseksi itse ongelma. Jos F(n) on perinteisen Fibonaccilukujonon n:s Continue reading
-
Neljännen asteen pentagrammifunktio
Tämän funktion on käsittääkseni keksinyt norjalainen Harald Totland. Kun pentagrammin kolmen pisteen kautta piirtää neljännen asteen polynomin, niin se kulkee myös pentagrammin kahden muun pisteen kautta. Piirretään säännöllinen viisikulmio ABCDE, pisteiden A ja B x-koordinaatit ovat yhtä suuret. Tässä A = (-1 ,0) ja B = (1 , 0). Piirrtetään viisikulmioon pentagrammi ACEBD. Piste F Continue reading
-
Fibonaccin sanoja artikkeli julkaistu Dimensiossa
Hannu Korhonen pyysi minua tutkimaan kanssaan Fibonaccin sanoja. Artikkelissa kerrotaan, mitä ne ovat ja miten tuottaa niitä GeoGebralla. Pohdimme artikkelissa myös binäärisistä Fibonaccisanoista muodostettujen lukujen kasvunopeutta. Päädymme arvaukseen, että kasvu lähestyy suurilla x:n arvoilla arvoa missä eli kultaisen leikkauksen luku. Artikkeli löytyy Dimension verkkosivulta https://www.dimensiolehti.fi/fibonaccin-sanoja/ Continue reading
