[edit. 21.2.20 Korjasin virheellisen kuvaajan.]
[edit. 22.2.20 Korjasin muutaman fysikaalisen virheen, kiitos Harri. Vaihdoin Worldometer-kuvan.]
Kun menet jollekin sivulle, joka esittää tietoa kuvaajina, niin usein törmäät tilanteeseen, että kuvaajan asteikot ovatkin logaritmisia. Miksi? Mitä koronaviruksen etenemistä esittävillä sivustoilla kuolleiden määrän logaritmi kertoo?
Minusta yksi kauneimmista tilastollisista esityksistä on Hertzsprung–Russell -diagrammi. Tähtitieteilijöillä on siitä monia eri versioita, mutta perinteisesti vaaka-akselilla on tähden pinnan väri sinisestä punaiseen ja pystyakselilla tähden absoluuttinen luminositeetti eli säteilyteho. Koska tähden pintalämpötila on sen pintalämpötilan mitta, niin loppujen lopuksi vaaka-akselilla onkin pintalämpötilan logaritmi oikealta vasemmalle eli mitä kuumempi tähti, niin sitä enemmän vasemmalla se on. Pystyakseli luminositeetti eli säteilyteho kertoo, kuinka moninkertainen tähden säteilyteho on Auringon tehoon (3,9·10^26 W) verrattuna. HR-diagrammissa pystyakseli on suhteellisen tehon logaritmi. Näin Aurinkomme sattuu mukavasti diagrammin keskialueelle.
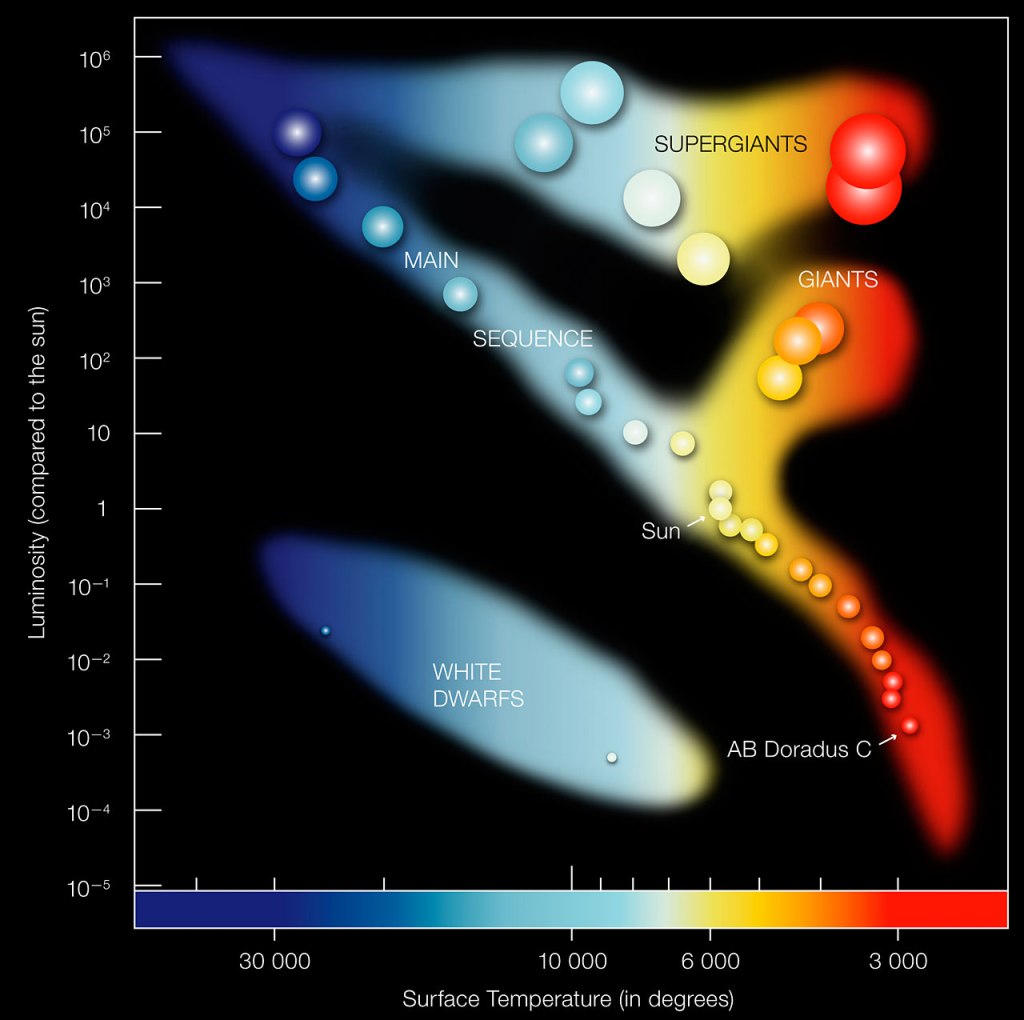
lähde ESO: https://www.eso.org/public/images/eso0728c/
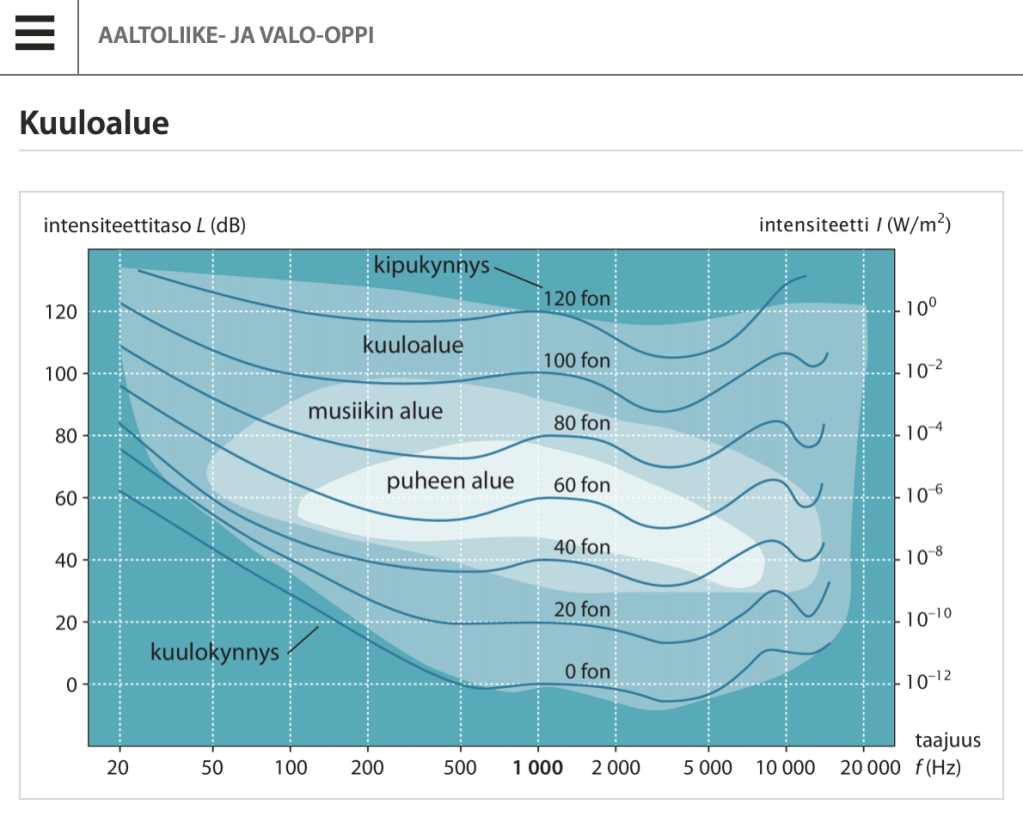
Kuuloalueen kuvaaja on fysiikan opiskelijoille tuttu kuvaaja MAOL taulukot -kirjassa. Siinä vaaka-akselilla on taajuus logaritmisella asteikolla ja pystyakseli on äänen intensiteettitaso desibeleinä, joka on suoraan verrannollinen äänen tehosuhteen logaritmiin.
Gapminder sivustolla on valtavasti eri valtioihin liittyvää tilastotietoa. Aineistojen aikasarjoja voi tutkia myös logaritmisilla asteikoilla. Kuvassa on vaaka-akselilla BKT/asukas eri maissa ja pystyakselilla odotettavissa oleva elinikä. Itse asiassa myös valtioita kuvaavien ympyröiden säde on logaritminen.
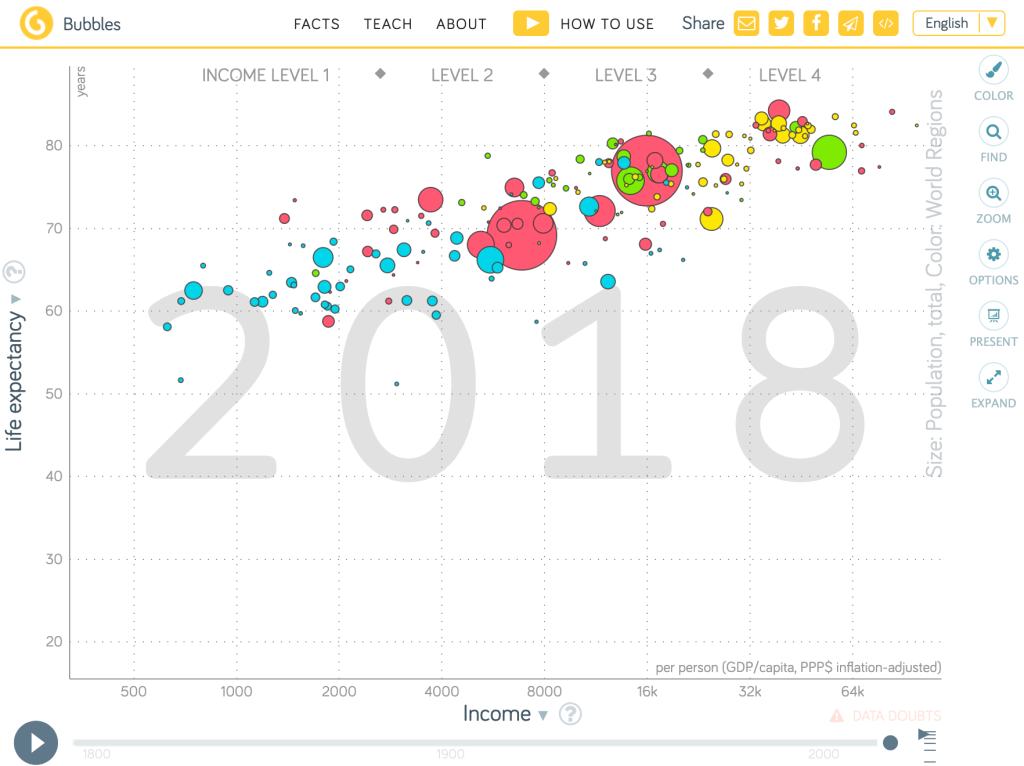
Lähde Gapminder sivu https://www.gapminder.org/tools/#$state$time$value=2018;;&chart-type=bubbles
Worldometer-sivustolla voi seurata korona-viruksen kuolleiden kokonaismäärää logaritmisella asteikolla.
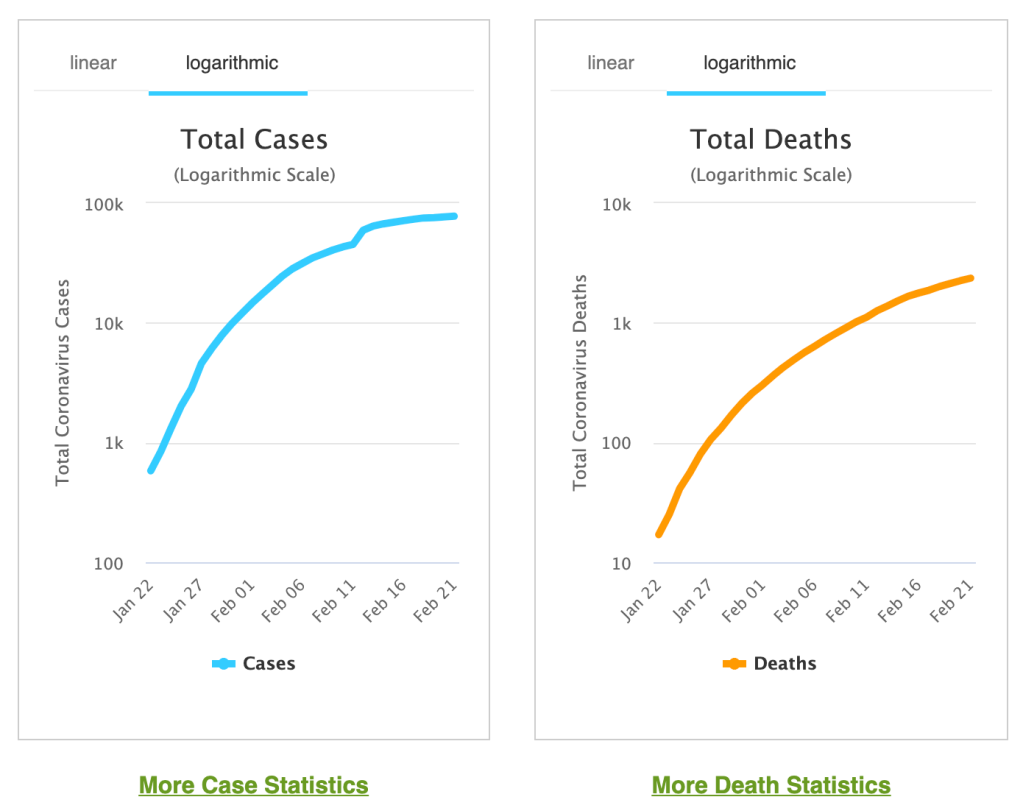
polynomiaalinen ja eksponentiaalinen kasvu
Tutkitaan esimerkkien avulla, miten akseleiden muuttaminen näkyy polynomeilla ja eksponenttifunktiolla. Käytän tässä tarinassa 10-kantaista logaritmia, sillä sitä käytetään yleensä kansantajuisissa taulukoissa. Tällöin näkee alkuperäisten lukujen suuruusluokan mukavasti. 10-kantainen logaritmi kun kertoo luvun nollien lukumäärän tyyliin lg(1000) = 3.
Lukiomatikassa tutkitaan yleensä aritmeettista tai geometrista lukujonoa. Aritmeettisessa lukujonossa kahden lukujonon peräkkäisen erotus pysyy vakiona ja geometrisessä suhde. Jos lukujonoja ajattelee funktioina siten, että järjestysluku on muuttuja x, niin aritmeettinen lukujono on 1. asteen polynomi f(x) = k x + b ja geometrinen lukujono on eksponenttifunktio g(x) = a·q^x.
On suhteellisen helppoa osoittaa, että jos k, n, a ja q > 1, niin a·q^x > k x^n kunhan x on riittävän iso. Eli eksponentiaalinen kasvu ohittaa aina jossain vaiheessa polynomiaalisen kasvun.
Kun pohditaan kasvunopeutta, niin ei yleensä välitetä polynomien a….. muista kuin korkeimman asteen termistä. Yleensä myös yleisen potenssifunktion tyyliin 2.5 x^1,23 kasvua kutsutaan polynomiseksi, vaikka 1,23 ei olekaan luonnollinen luku (0, 1, 2, 3, …).
Otetaan esimerkiksi funktiot f(x) = 3*x^2 ja g(x) = 3*2^x. Funktio f on toisen asteen polynomi ja g eksponenttifunktio, jonka kasvukerroin (taulukkokirjassa talousmatematiikan kohdalla korkotekijä) q = 2.
loglog
Luon GeoGebrassa taulukon, jossa kaksi ensimmäistä saraketta ovat x ja f(x), seuraavat kaksi x ja lg(f(x)) ja kolmannessa parissa lg(x) ja lg(f(x)) Luon noista kolme pistelistaa nimetä linlin, linlog ja loglog. Punainen pistelista lililin on normaali ”koordinaatisto”, vihreässä on normaali x ja y-koordinaatti on lg(f(x)). Sinisessä loglog-pistelistassa molemmista on otettu logaritmi.


Kuvaajasta nähdään, että vihreä lukujono kasvaa todella hitaasti, mutta sininen näkyisi kasvavan suoraviivaisesti. Kun sinisiin pisteisiin sovitetaan suora komennolla
p(x) = SovitaPolynomi(loglog, 1)
havaitaan, että suoran kulmakerroin on 2 eli alkuperäisen polynomimme asteluku. Vakiotermin avulla päästään kertoimeen laskemalla CASissa
10^0,47712
-> 2,99999
Tai jos olet lukenut edellisen artikkelini ”Arvojen poimiminen listoista ja yhtälön ratkaisuista GeoGebrassa”
10^Alkio(Kertoimet(p), 2)
-> 3
Jätän lukijalle todistettavaksi, että jos f(x) = k x^n, niin loglog-koordinaatistossa syntyy suora, jonka kulmakerroin on n ja k = 10^(suoran vakiotermi).
linlog
Tutkitaan samalla tavalla eksponenttifunktiota
g(x) = 3*2^x
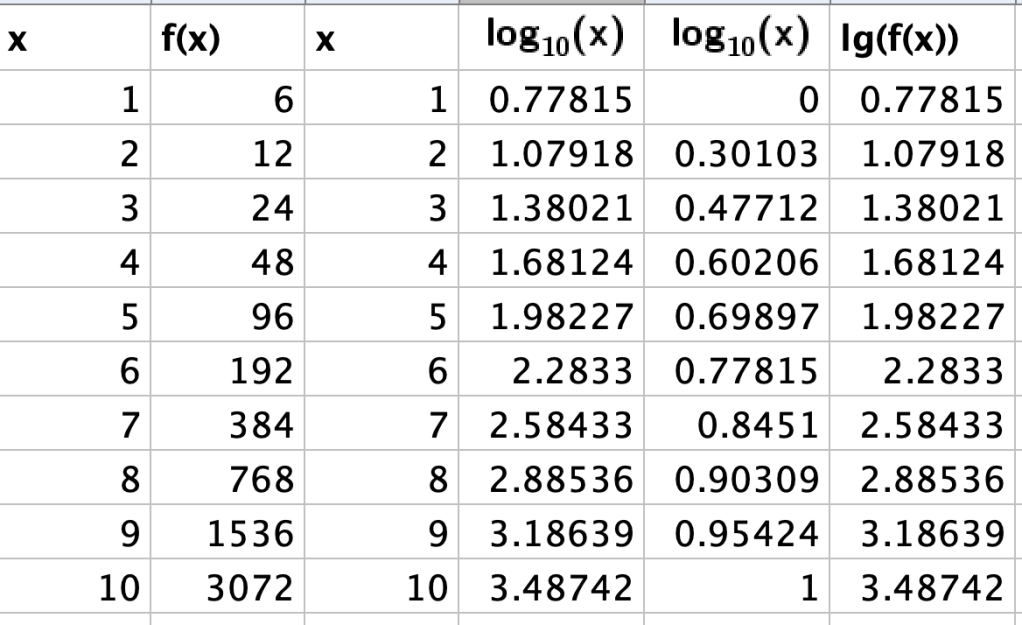

Nyt vihreä loglog-käyrä ei ole suora, mutta linlog on. Sen yhtälöstä saadaan
10^0.30103
-> 2
10^0.47712
-> 3
Jätän taas lukijalle pohdittavaksi miksi eksponenttifunktiolla a q^x loglog-sovituksen suoran yhtälöllä q = 10^kulmakerroin ja a = 10^vakiotermi.
Lisäksi voit pohtia, minkä tyyppinen käyrä sininen loglog lukujono on.
lopuksi
Toki lukusarjoja olisi voinut alun perikin tutkia käyttämällä GeoGebran sovita-komentoja. Silti monessa tapauksessa, kun tutkitaan lukusarjoja, joiden kasvunopeuksia ei tunneta, on logaritmisten akseleiden käyttö aika kätevää.
Vielä muistutukseksi.
Jos linlog- koordinaatistossa on suora, niin se kertoo eksponentiaalisesta a·q^x kasvusta.
Jos loglog -koordinaatistossa on suora, niin se kertoo polynomiaalisesta (potenssifunktio) k·x^n kasvusta.
Mitä Worldometer-kuvaaja kertoo? Koronavirukseen sairastuneiden ja kuolleiden kokonaismäärä ei tämän datan perusteella kasva eksponentiaalisesti. Palannen tähän aiheeseen, kun käytössä on pidempi aikasarja ja useammasta eri valtiosta.

3 Replies to “Miksi kuvaajissa esitetään tietoa logaritmisella asteikolla?”