[edit.9.11.18  korjasin pari kirjoitusvirhettä sekä tyylejä
20.1. 20 poistin mb8 otsikosta sillä se liittyy vanhaan ops:iin]

Tämä ohje toimii ainakin GeoGebra 5.0.498.0 ja 6.0.498.0-versioista lähtien. Esimerkiksi nCr-komento tuli kesällä 2018 versioissa 5/6.0.493.0.

Tärkeimmät työkalut kurssilla ovat tietysti GeoGebran Yhden muuttujan analyysi-, Kahden muuttujan regressioanalyysi- työkalut sekä Todennäköisyyslaskuri. Kaksi ensimmäistä liittyvät lukujen tutkimiseen taulukkolaskennassa (palataan niiden käyttöön myöhemmin) ja Todennäköisyyslaskuri löytyy GeoGebran Näytä-valikosta. Laskurin avulla voi ratkoa paljon erilaisia tehtäviä liittyen jatkuviin ja diskreetteihin jakaumiin. Näiden kolmen työkalun käyttöön kannattaa tutustua ensin. Seuraavat komennot ovat lähinnä lisäapuna mikäli joutuu käsittelemään tilastollista dataa työkalujen ulkopuolella.

Esitän seuraavaksi joitakin tärkeimpiä komentoja, joita voi käyttää kurssin tehtävien ratkaisussa. Komennot on kirjoitettu GeoGebra CASiin.

Sovituksiin liittyvät komennot löytyvät artikkelistani Sovituskomennot GeoGebrassa https://mikonfysiikka.wordpress.com/2018/10/15/sovituskomennot-geogebrassa/. Siellä on myös esitetty Kahden muuttujan regressioanalyysi- työkalu.

Tilastollisia tunnuslukuja

Luodaan ensiksi pieni lista, jossa on lukuja.

Listan lukujen lukumäärä, keskiarvo, mediaani, keskihajonta ja otoskeskihajonta saadaan komennoilla:

lista:={1,1,2,3,3,3,4,5}
-> lista:={1, 1, 2, 3, 3, 3, 4, 5}

Pituus(lista)
-> 8

Keskiarvo(lista)
≈ 2.75

Mediaani(lista)
-> 3

Keskihajonta(lista)
-> 1.3

Otoskeskihajonta(lista)
≈ 1.39

GeoGebran CAS-tilassa GeoGebra korvaa Keskiarvo-komennon sen lyhenteellä keskar, Keskihajonnan lyhenteellä keskha ja Otoskeskiarvon lyhenteellä stdevp. Korvaus liittynee uusien appien toimintaan.

Luodaan pistelista

pisteet≔ {(1, 2), (2, 4), (3, 3), (4, 5), (5, 7), (6, 7), (7, 9), (8, 6), (9, 11), (10, 13)}
-> pisteet≔ {(1, 2), (2, 4), (3, 3), (4, 5), (5, 7), (6, 7), (7, 9), (8, 6), (9, 11), (10, 13)}

Regressiosuoran yhtälö ja korrelaatiokerroin saadaan komennolla

SovitaSuora(pisteet)
-> y = 1.06x + 0.87

Korrelaatio(pisteet)
-> 0.92

Mikäli olisi haluttu vaihtaa regressiosuoran määräämisessä x– ja y-koordinaattien paikkaa olisi pitänyt käyttää SovitaX-komentoa.

SovitaSuoraX(pisteet)
-> y = 1.26x – 0.22

Pisteiden x-koordinaattien ja y-koordinaattien keskiarvot ja keskihajonnat:

KeskiarvoX(pisteet)
-> 5.5

KeskiarvoY(pisteet)
-> 6.7

KeskihajontaX(pisteet)
-> 2.87

KeskihajontaY(pisteet)
-> 3.32

Seuraavassa kuvassa on esitetty pistelista pisteet, piste K on x-koordinaattien ja y-koordinaattien keskiarvopiste, pisteen L koordinaatit on saatu lisäämällä x-koordinaattien ja y-koordinaattien keskihajonnat keskiarvopisteen koordinaatteihin. Pisteet N, O ja M on luotu samalla menetelmällä lisäämällä tai vähentämällä keskiarvoja.

Todennäköisyyteen ja jakaumiin liittyviä komentoja

Kertomafunktio toimii tutusti huutomerkillä

5!
-> 120

Binomijakauma

Binomikertoimet eli kombinaatiot eli (5 alla 2) -merkintä saadaan nCr- tai Binomikerroin-komennolla.

nCr(5, 2)
->  10

Toistokokeen binomitodennäköisyys  lasketaan Binomijakauma-komennolla. Komento toimii hieman eri tavalla CAS:issa ja Syöttökenttää käytettäessä.

Heitetään noppaa 5 kertaa. Millä todennäköisyydellä tulee tasan 3 ykköstä? Nyt n = 5, p = 1/6 ja k = 3.

Syöttökentässä komento

Binomijakauma(5, 1 / 6)

piirtää piirtoalueelle jakauman kuvaajan

Jakauman kertymäfunktio piirretään komennolla

Binomijakauma(5, 1 / 6, true)

Sekä CASissa, että Syöttökentässä kysytty todennäköisyys lasketaan komennolla

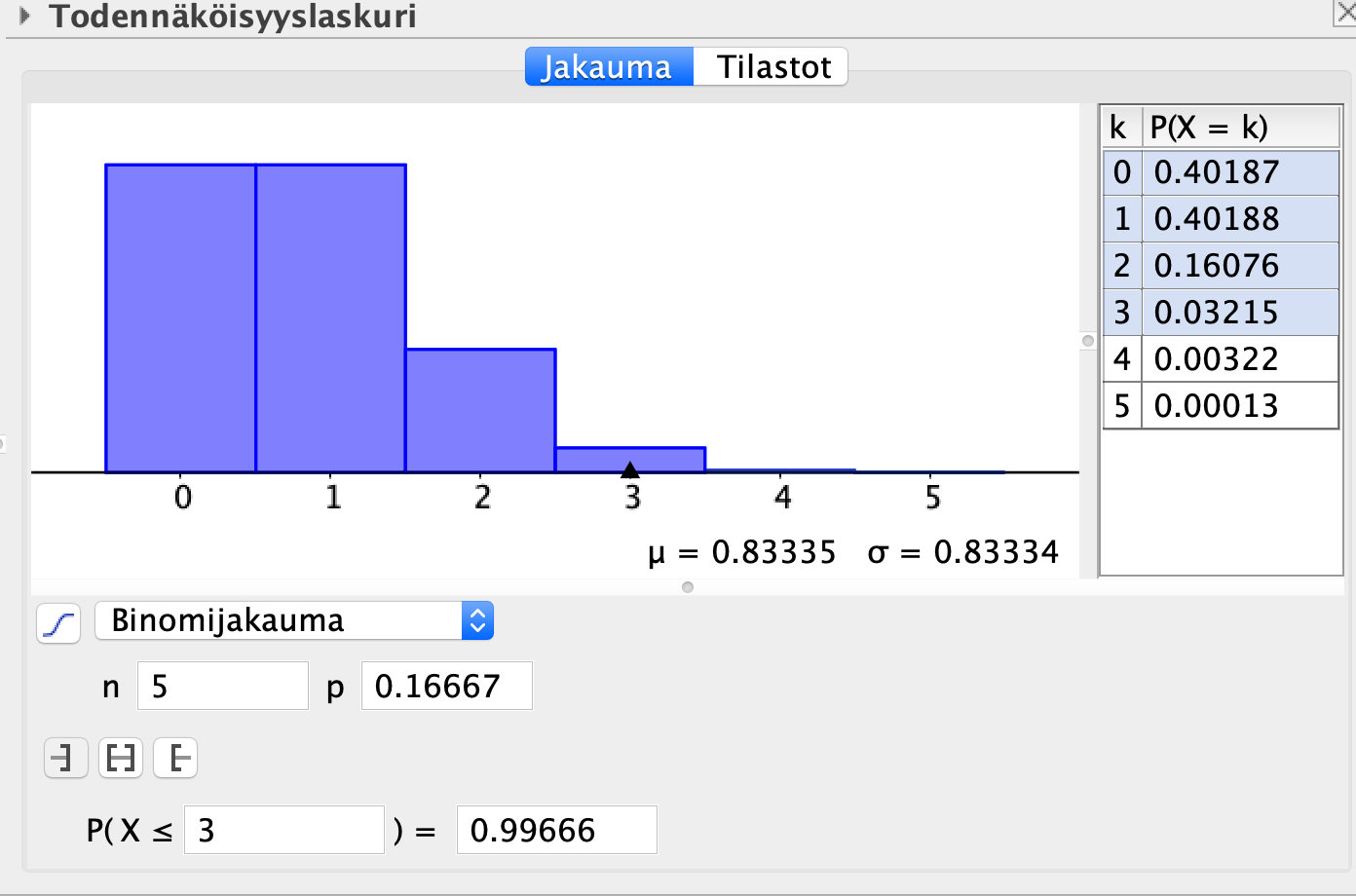
Binomijakauma(5, 1/6, 3, false)
≈ 0.03215

Kertymäfunktion arvo saadaan komennolla

Binomijakauma(5, 1/6, 3, true)
≈ 0.99666

Vertaa lukuja Todennäköisyyslaskurin tulokseen.

Poissonjakauma

Poissonjakauma -komento toimii samalla logiikalla kuin Binomijakauma.

Oletetaan, että pitkäaikaisen kokemuksen mukaan opettaja kertoo huonon vitsin oppitunnilla keskimäärin 3,3 kertaa. Millä todennäköisyydellä hän kertoo huonon vitsin tasan kaksi kertaa, jos huonojen vitsien kertominen on Poissonjakautunut?

Syöttökentässä komento

Poisson(3.3)

tuottaa jakauman piirtoalueelle. Kertymäfunktio syntyy komennolla

Poisson(3.3, true)

Tehtävän ratkaisu eli kun x = 2 saadaan komennolla

Poisson(3.3, 2, false)

-> 0.20083

ja kertymäfunktion arvo, kun x ≤ 2

Poisson(3.3, 2, true)

-> 0.35943

Vertaa Todennäköisyyslaskurin kuvaan.

Jatkuvat jakaumat

Jatkan tarinaa lähipäivinä, nyt alan odottelemaan isänpäivää.

Hyvää isänpäivää lukijoille.